Définition: Association (M-L)

M et L non identifiés par des réactions caractéristiques. Leurs propriétés analytiques sont dissimulées.

Donneur de particule

(1)  

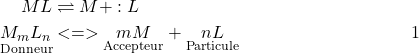
• Mononucléaire
• Polynucléaire
• Ligands = Coordinats
• Indice de coordinance: L M
• Structure (gaz inertes)

Différents types de Complèxes

• Simples : ex:
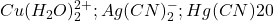
• Chélates : ex: 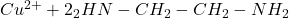(éthylène diamine, ac. Aminés (zwitterionique+-), dipyridine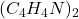

Autres chélateurs:

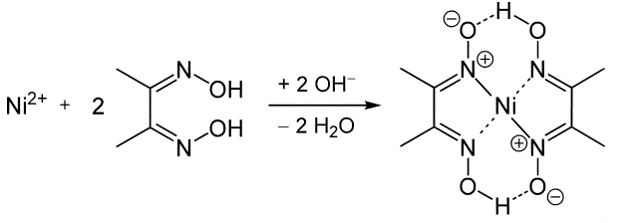
• Hydroxy8quinoléine (Mg du Sang; Al de l’eau pour hémodialyse)
• Diméthylglyoxine (Ni)
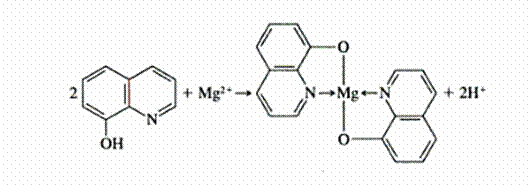
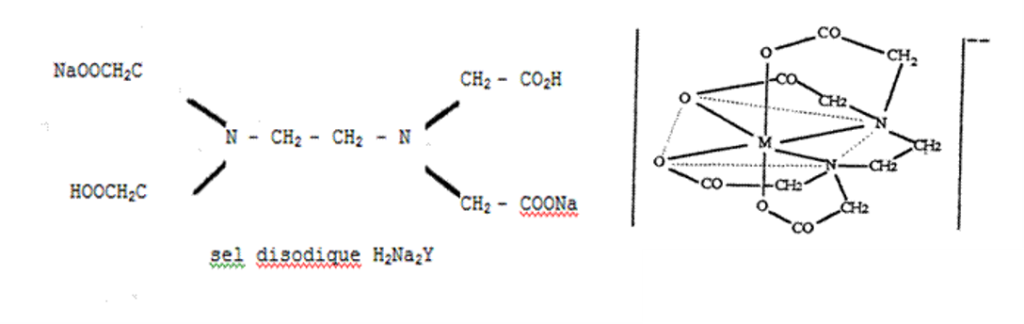
• EDTA (Ca, Mg, Fe…)
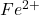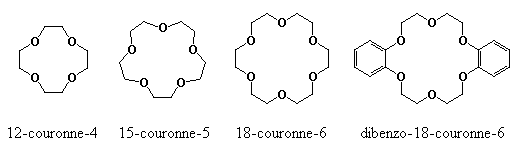
• Glyoxal (Ca); Thiourée (Bi); Phénanthroline ( ); Indicateurs (NET…)
• Éther couronne (piégeage sélectif des ions légers) (Voir Pharmacopée)

NB: Chélates naturels: Chlorophylles ( ); hémoglobines ( )

Ex. de formation de Complexes:

Complexe M- EDTA :

Éthers couronnes : Li, Na, K :

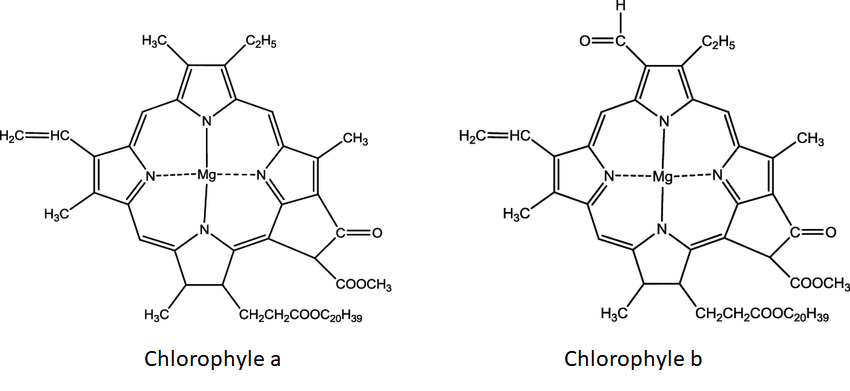
Chlorophylles : sont constituées d’un noyau tétrapyrrolique avec un magnésium en son centre, et estérifié avec un alcool à très longue chaine en C20 (le phytol).

Aspects qualitatifs

• Complexe parfait : pas de dissociation ex: 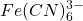= (Ferricyanure) , 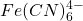= (Ferrocyanure)
• Complexe imparfait : dissociation partielle. ex:

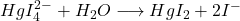
Aspects quantitatifs: (constante de stabilité)

un complexe est toujours partiellement dissocié:

• Constante de stabilité
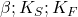
• Constante de dissociation:

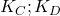
Exemple:

(2)  

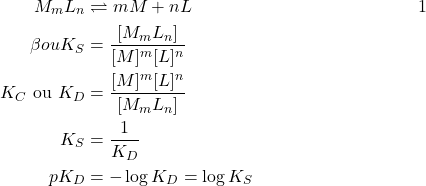
K évalue la force des complexes

• Plus 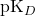grand: plus l’accepteur est fort donc le complexe est stable.
• Plus 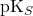petit: plus le complexe est stable.

Complexes successifs

(3)  

Si n supérieur à 1, addition successive de L:

(4)  

(5)  

(6)  

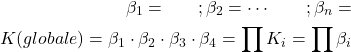
(7)  

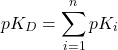
Réactions secondaires

exemple:

(8)  

On acidifie:

(9)  

• Réactions secondaires au niveau de M:
  • OH ML; ML2…..
  • M
  • L MOH; M(OH)2 …..
• Réactions secondaires au niveau de L:
  • H ML; ML2 ……
  • L
  • M HL; H2L …..

Remarque:

(10)  

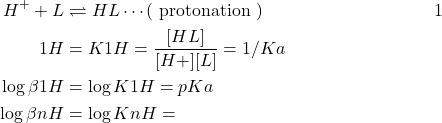
Ex:

(11)  

Dissociation des Complexes; notion de pL

prévision des réactions:

(12)  

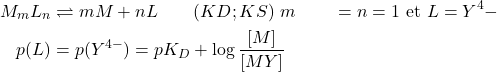
Échelle de pKd

*** QuickLaTeX cannot compile formula:
  \begin{table}     ntering     \begin{tabular}{lllll} Donneur Fort    &   {{LiY^3-}}  & {Li^+} &  &  $pK_D = 2,8$ \\      &{MgY^{2-}}  & { Mg^{2+}}&  &  $pK_D = 8,7$\\      & {ZnY^{2-}}  &  {Zn^{2+}}&  &  $pK_D = 16,3$ \\      &{FeY^-}  &  {Fe^{3+}}& Accepteur Fort &  $pK_D = 25,1$\\  \end{tabular}  \end{table}  

*** Error message:
Not in outer par mode.
leading text: $  \begin{table}     n
Undefined control sequence \@currbox.
leading text: $  \begin{table}     n
Missing number, treated as zero.
leading text: $  \begin{table}     n
Missing $ inserted.
leading text: ...tabular}{lllll} Donneur Fort    &   {{LiY^
Extra }, or forgotten $.
leading text: ...ular}{lllll} Donneur Fort    &   {{LiY^3-}
Extra }, or forgotten $.
leading text: ...lar}{lllll} Donneur Fort    &   {{LiY^3-}}
Missing } inserted.
leading text: ...}{lllll} Donneur Fort    &   {{LiY^3-}}  &
Extra }, or forgotten $.
leading text: ...}{lllll} Donneur Fort    &   {{LiY^3-}}  &
Missing } inserted.
leading text: ...}{lllll} Donneur Fort    &   {{LiY^3-}}  &
Extra }, or forgotten $.
leading text: ...}{lllll} Donneur Fort    &   {{LiY^3-}}  &

Ex:

(13)  

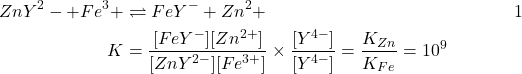
[FeY- pKD-2 pKD pKD+2 Fe3+ p(Y4-)

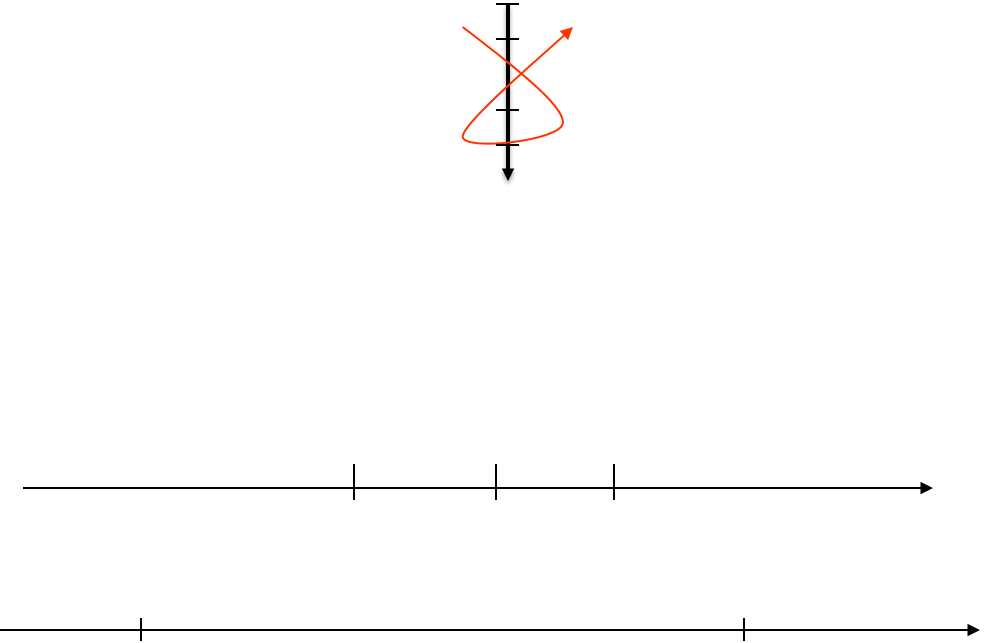
Déplacement de M1L peu stable par M2 pour former très stable

Influence de la concentration sur Kd:(ML; et )

*** QuickLaTeX cannot compile formula:
  \begin{table}     ntering     \begin{tabular}{ccccc}   ML& $\rightleftharpoons$    & M & + & L  \\      {C_0}&     & - &  & - \\    ${C_0}(1-\alpha )$&    &  $\alpha C_0$ &  & $\alpha C_0$ \\  \end{tabular}  \end{table}  

*** Error message:
Not in outer par mode.
leading text: $  \begin{table}     n
Undefined control sequence \@currbox.
leading text: $  \begin{table}     n
Missing number, treated as zero.
leading text: $  \begin{table}     n
Missing $ inserted.
leading text: ...tleftharpoons$    & M & + & L  \\      {C_
Extra }, or forgotten $.
leading text: ...eftharpoons$    & M & + & L  \\      {C_0}
Missing } inserted.
leading text: ...ftharpoons$    & M & + & L  \\      {C_0}&
Extra }, or forgotten $.
leading text: ...ftharpoons$    & M & + & L  \\      {C_0}&
Missing } inserted.
leading text: ...ftharpoons$    & M & + & L  \\      {C_0}&
Extra }, or forgotten $.
leading text: ...ftharpoons$    & M & + & L  \\      {C_0}&
Missing } inserted.
leading text: ...ftharpoons$    & M & + & L  \\      {C_0}&

• Plus 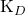grand, plus 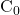petit plus le complexe se dissocié.
• Un excès de L favorise la formation de ML

Relation entre structure et stabilité

Ion coordinateur

Petite dimension; sym. et charge élevée;
Faible électronégativité.

Ligand

• Minéraux : pas de règle générale (pouvoir donneur)
• Chélates:
  • Rapport (L/M) ex: 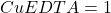et ;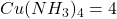
  • Nombre de cycles;
  • Nombre d’atomes du cycle (hexa.,penta.);
  • Nature des atomes donneur (N, O et S, P, As)

NB: Complexation: essais limites , (détermination des métaux lourds)