Applications

Dosage en milieu neutre : Méthode de Mohr

Principe et conditions

La méthode de Mohr s’opère de manière directe en présence d’ions chromates (CrO₄^2-) qui jouent le rôle d’indicateur de fin de réaction. Le dosages est réalisé à pH compris entre 6 et 10.

1. A un pH < 6 , le chromate (CrO₄^2-) est soluble selon la réaction suivante: \begin{align} Ag_2CrO_4 \rightleftharpoons {2} Ag^+ + CrO_4^{2-} \end{align}
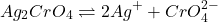
2. A un pH acide la solubilité S augmente: \begin{align} CrO_4^{2-} + H^+ &\rightleftharpoons HCrO_4^{-} \qquad {\text{Système déséquilibré} }. \end{align} Pour rétablir le produit de solubilité (Ps), les chromates d’argent (Ag₂CrO₄) se dissolvent, donc l’indicateur ne joue plus son rôle.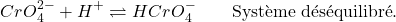
3. A un pH >10 , il y a formation d’hydroxyde d’argent (AgOH): Ag⁺ (réactif) précipite : \begin{align} 2Ag^+ + 2OH^- \rightleftharpoons {2}AgOH \rightleftharpoons Ag_2O + H_2O \end{align}

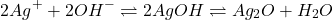
un peu du réactif est consommée dans la réaction, alors le pH de la prise d’essai doit être corrigé.

• Si l’échantillon est acide, on opère en présence de carbonate de sodium {Na_2CO_3}.
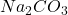• Si l’échantillon est basique, on acidifie au préalable par l’acide acétique {CH_3COOH}.

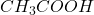Remarques:

• Iodure (I^–): interférence de colorations de Ag₂CrO₄ et AgI (indicateur= amidon iodé).
• Les cyanures (CN^–) en milieu acide se transforment en HCN volatil.
• Les ions gênants : phosphates (PO₄^3-), arséniates (AsO₄^3-) et ammoniac (NH₃) … précipitent en même temps que les halogénures, ainsi que les cations qui réagissent avec les chromates (CrO₄^2- ) tels que les ions de Plomb (Pb²⁺), Barium (Ba²⁺), Strontium (Sr²⁺)… doivent être éliminer sous forme de sulfates (SO₄^2-) avant le dosage.

Réactions

Soit X^– l’halogénure à analyser :
\begin{align} Ag^+ + X^- &\rightleftharpoons AgX \\ 2Ag^+ + CrO_4^{2-} &\rightleftharpoons Ag_2CrO_4 \end{align}

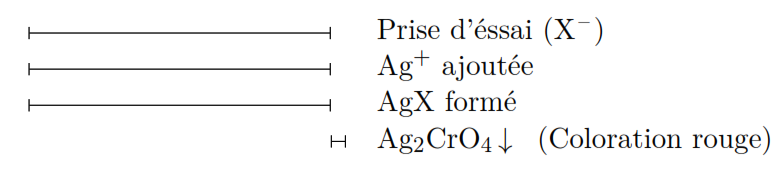
L’apparition de la coloration rouge indique la fin du dosage.
Cette méthode n’est pas utilisée pour le dosage des ions iodure à cause de l’interférence des colorations des composés formés au cours du dosage à savoir : chromate d’argent (Ag₂CrO₄) et l’iodure d’argent (AgI).

L’échantillon ne doit pas contenir des ions gênants tels que les phosphates (PO₄^3-)et les arséniates (AsO₄^3-) qui précipitent en même temps que les halogénures, ainsi que les cations qui réagissent avec les chromates tels que Pb²⁺, Ba²⁺ ou Cr²⁺.
Ces ions peuvent être éliminés au préalable sous forme de sulfates.

Indicateur

A quelle concentration [CrO₄^2-], Ag₂CrO₄ commence à précipiter ?

Exemple : dosage des chlorures

Au point équivalent, les ions Ag⁺ présents en solution proviennent de la dissolution partielle de AgCl selon :
\begin{align} AgCl &\rightleftharpoons Ag^+ + Cl^- \quad &Ps_1 &= 10^{-10}\\ \textbf{l’indicateur est obtenu par:} \\ 2Ag^+ + CrO_4^{2-} &\rightleftharpoons Ag_2CrO_4 \quad &Ps_2 &= 10^{-12} \end{align}

La réaction avec l’indicateur :
\begin{align} Ps_2 &= [Ag+]^2.[CrO_4^{2-}] \\ [CrO_4^{2-}] &= \dfrac{Ps_2}{[Ag^+]^2 }= \frac{Ps_2}{Ps_1} = 10^{-2} M \end{align}

• Si [CrO₄^2-]<10^-2: Ag₂CrO₄ précipite après le point d’équivalence = erreur par excès.
• Si [CrO₄^2-] >10^-2: Ag₂CrO₄ précipite avant le point d’équivalence = erreur par défaut.

La concentration de l’indicateur joue un rôle important (précision du dosage). Une solution de K₂CrO₄ à 10 % est alors utilisée, pour que la concentration soit a peu prés de 10^-2M à l’équivalence.

Dosage en milieu acide : Méthode de Charpentier-Vollard

Principe et conditions

Cette technique indirecte repose sur un dosage en retour. La solution à doser est mise en présence d’une quantité connue et excédentaire d’ions Ag⁺ , en milieu nitrique.

L’excès du nitrate d’argent est dosé par une solution antagoniste titrée de thiocyanate d’ammonium ou de potassium. Les ions ferriques jouent le rôle d’indicateur de fin de réaction.

Le dosage doit être effectué à pH inférieur à 2 .
Si le pH est supérieur à 2 les ions ferriques (Fe³⁺) précipitent sous forme d’hydroxyde de fer (Fe(OH)₃ ) et ne jouent plus leur rôle d’indicateur.

Application au dosage des halogénures (X^–):

Réactions

\begin{align} Ag^+ + X^- &\rightleftharpoons AgX \\ Ag^+ + SCN^- &\rightleftharpoons AgSCN \\ Fe^{3+} + SCN^- &\rightleftharpoons [FeSCN]^{2+} \end{align}

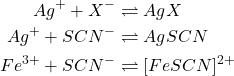
Indicateur

Solution aqueuse d’alun ferrique à 12 %. La fin du
dosage correspond à l’apparition d’une coloration rouge
sang due à la formation du complexe [FeSCN]²⁺

L’apparition de la coloration rouge indique la fin du dosage.

Cette méthode n’est appliquée au dosage des iodures et des cyanures que sous certaines conditions évidentes.

L’acidification de la prise d’essai à l’aide de l’acide nitrique risque d’oxyder partiellement les ions iodure I^– en iode I₂ qui échapperaient au dosage. De même, les ions cyanure sont transformés en acide cyanhydrique volatil. Pour ces ions, on commet une erreur par défaut.

Pour y remédier, on opère en milieu nitrique dilué et surtout on n’acidifie qu’après l’ajout du nitrate d’argent, ce qui permet de protéger les ions iodure et cyanure de l’action oxydante de l’acide nitrique puisque ces ions se trouvent déjà engagés sous forme de précipités stables et donc dissimulés.

Les ions gênants au cours de ce dosage sont ceux qui précipitent avec SCN^–, tels que Ca²⁺, Ba²⁺, Sr²⁺ … Ces derniers doivent être éliminés au préalable de la prise d’essai.

Les ions en excès s’adsorbent à la surface du précipité AgSCN, ce qui les rend inaccessibles au dosage et il est nécessaire d’agiter énergiquement pour libérer ces ions au cours du titrage.

Des difficultés supplémentaires peuvent résulter de la précipitation de deux composés, qui peuvent interférer l’un avec l’autre. Par exemple, le dosage des chlorures implique la solubilité du chlorure d’argent d’une part et celle du thiocyanate d’argent d’autre part.
\begin{align}Ag^+ + Cl^- &\rightleftharpoons AgCl & Ps_1&=10^{-10} \\ Ag^+ + SCN^- &\rightleftharpoons AgSCN & Ps_2&=10^{-12} \end{align}

Une simple comparaison des Ps indique que AgSCN précipite en premier.

Protocole opératoire

On forme d’abord AgCl en premier par Ag⁺ en excès, puis en second lieu, AgSCN au cours du dosage de l’excès de Ag⁺ par SCN^–.

Au deuxième point équivalent, le réactif SCN^– ne rencontre plus de Ag⁺ libre, mais Ag⁺ provenant de AgCl, qui tend à se dissoudre pour rétablir Ps₁.

Pour résoudre ce problème, 2 possibilités:

1. Éliminer le premier précipité par filtration, puis doser l’excès de Ag⁺ dans le filtrat, mais cette opération s’accompagne toujours d’une petite perte inévitable au cours du lavage du précipité.
2. Protéger le premier précipité en ajoutant des substances organiques qui ont la propriété de s’adsorber à la surface. On utilise souvent le nitrobenzène ou l’acide amylique en faible quantité (1 à 2 %).

Dosage par la méthode de Paneth-Fajans :

Principe

Cette méthode est basée sur le dosage argentimétrique utilisant des indicateurs d’adsorption pour la mise en évidence du point équivalent.

Cette adsorption ne s’effectue pas d’une manière aléatoire ; mais elle fait intervenir un phénomène de surface bien connu. Ce sont les ions, anions ou cations, qui donneraient les sels les moins solubles avec l’un des ions constitutifs du précipité qui sont les plus adsorbés.

On opère en présence de dextrine ou de gélose qui sont des colloïdes pour maintenir des surfaces aussi grandes que possible.

Tous les dosages décrits par Mohr et Charpentier-volhard peuvent être réalisés par cette méthode.

Indicateurs

Deux types d’indicateurs existent, selon que l’on dose X^– par Ag⁺ ou l’inverse. Ces indicateurs ont des colorations à l’état libre qui différent de celles lorsqu’ils sont adsorbés.

1. Indicateurs anioniques : On utilise la fluorescéine et ses dérivés la dichlorofluorescéine et la tetrabromofluorescéine (éosine) pour le dosage des anions par les cations. Ces trois indicateurs couvrent un domaine de pH du dosage allant de 9 à 1 selon l’acidité et l’espèce à titrer.
2. Indicateurs cationiques : On utilise souvent la rhodamine qui est un bon indicateur pour le dosage des ions Ag⁺ par X^– .

Titrages

Dosage de Cl^– par Ag⁺ (indicateur: Fluorescéine-)

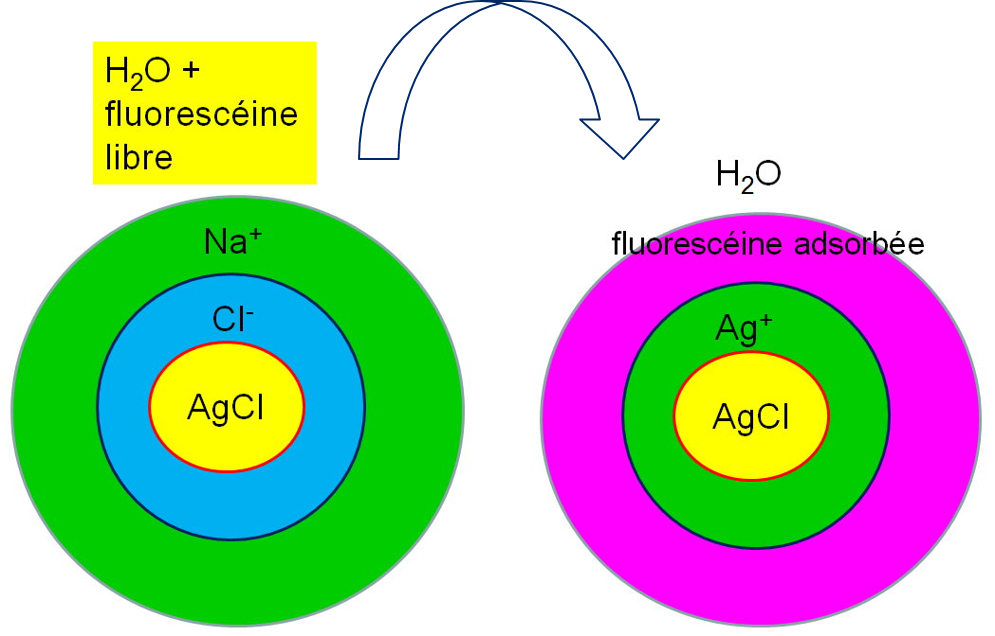
• Avant l’équivalence, la solution contient des ions chlorures en excès, AgCl qui s’est formé et l’indicateur. Les ions Cl^– forment une première couche de charge négative autour de AgCl pour conserver la neutralité électrique, puis les contres ions Na⁺ forment une seconde couche de charge positive et enfin, une dernière couche est constituée par des molécules neutres du solvant. La fluorescéine, colorant anionique est repoussé par le précipité et reste à l’état libre en solution. La coloration du milieu réactionnel est jaune. On a alors l’enchaînement suivant des différentes couches: Schéma: (AgCl – première couche de Cl^–– deuxième de Na⁺– troisième de H₂O puis la Fluorescéine libre (jaune).
• À l’équivalence, les ions Cl^– sont consommés. AgCl est en présence de Na⁺. Dès que le point équivalent est dépassé, l’ajout d’un petit excès de Ag⁺ forme la première couche chargée positivement autour des grains du précipité. L’indicateur anionique vient neutraliser les ions Ag⁺ en formant la seconde couche de charge négative, ce qui donne à la solution une coloration rouge. La dernière couche est formée comme précédemment par les molécules de l’eau. Le point équivalent correspond au virage du jaune au rouge. La coloration rouge est celle de l’indicateur adsorbé. L’enchaînement des couches est schématisé comme suit: Schéma: (AgCl ) première couche de Ag⁺ – deuxième fluorescéine adsorbée)-troisième de H₂O

Dosage de Ag⁺ par Cl^– (indicateur: Rhodamine)

Raisonnement similaire à l’exemple 1 :

• Avant l’équivalence, ce sont les ions Ag⁺ en excès qui forment la première couche; la deuxième couche formée par les ions nitrates réalisent la neutralité. Le solvant constitue la dernière couche. A ce stade du dosage, l’indicateur se trouve à l’état libre.
• Au-delà de l’équivalence, les ions Cl^– forment la première couche, l’indicateur cationique réalise la neutralité électrique en formant la seconde couche. Le point équivalent est donné par le virage du jaune orangé (indicateur libre) au rouge violet (indicateur adsorbé).

Cette méthode permet des titrages à pH très acide, (avantage par rapport aux 2 techniques précédentes).

Exemples de dosage :

• Chlorure de sodium
• Sels de rehydratation
• Chlorure de potassium
• Chlorobutanol

Dosages potentiométriques

Principe

Basé sur la détermination des E, potentiel d’équilibre donné par l’équation de Nernst, (système Ag/Ag^+) :
\begin{align} Ag \rightleftharpoons Ag^+ + e^- \qquad \qquad E= E^{\circ} + 0,06 \cdot\log[Ag^+] \end{align}

On utilise une électrode d’argent pour suivre à tout instant la [Ag⁺] ( phase aqueuse de cette suspension).

Elle est indicatrice des Ag⁺. On mesure \Delta E d’où 2 électrodes l’une indicatrice (électrode d’argent) et l’autre de référence (Potentiel fixe).

Dosages de Cl^– par Ag⁺(titrée)

Tableau récapitulatif du titrage

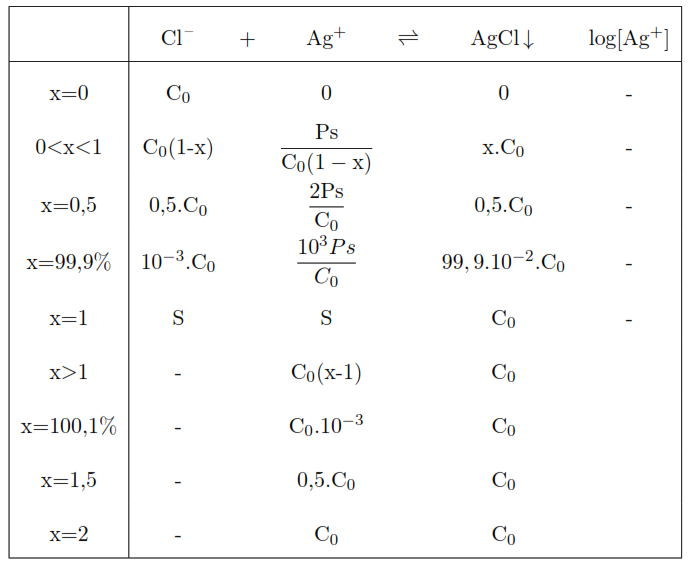
Expression de E=f([Ag⁺]) voir tableau

Avant l’équivalence

1. x=0 : à ce point, E mal défini.
2. 0 < x <1 : \begin{align}E = E^{\circ} + 0,06 \cdot \log [Ag^+] \end{align}. excès de Cl^– et une petite quantité de Ag⁺ de la dissociation de AgCl.

• Évaluons [Ag⁺]; Ps = [Ag⁺][Cl^-]
• On tire [Ag^+] = \dfrac{Ps}{[Cl^-} = \dfrac{Ps}{C_0(1-x)}

\begin{align}
\text{d’où }\qquad E_m = E^{\circ} + 0,06 \cdot \log Ps – 0,06 \cdot \log [C_0(1-x)] \label{avant_eq}
\end{align}

A l’équivalence

AgCl en solution saturée (x = 1):

Ps = [Ag^+] .[Cl^-] = S^2 d’où [Ag^+] = S = \sqrt{Ps}
\begin{align}
E_m = E^{\circ} + 0,03 \cdot \log {Ps}\label{a_equi}
\end{align}

Au delà de l’équivalence: (x >1)

AgCl en présence d’un excès de Ag⁺.

[Ag⁺] totale = [Ag⁺] provenant de la dissolution de AgCl, c’est à dire S ou encore \sqrt{Ps} et [Ag⁺] en excès soit C₀(x-1).
\begin{align}
E_m = E^{\circ} + 0,06 \cdot \log\left(\sqrt{Ps} + C_0(x-1)\right) \label{apres_eq}
\end{align}
\sqrt{Ps} est négligeable devant C₀(x-1)
\begin{align} \text{d’où }\qquad E_m = E^{\circ} + 0,06 \cdot \log \left(C_0(x-1)\right) \end{align}

Allure de la courbe potentiométrique E_m = f (x)

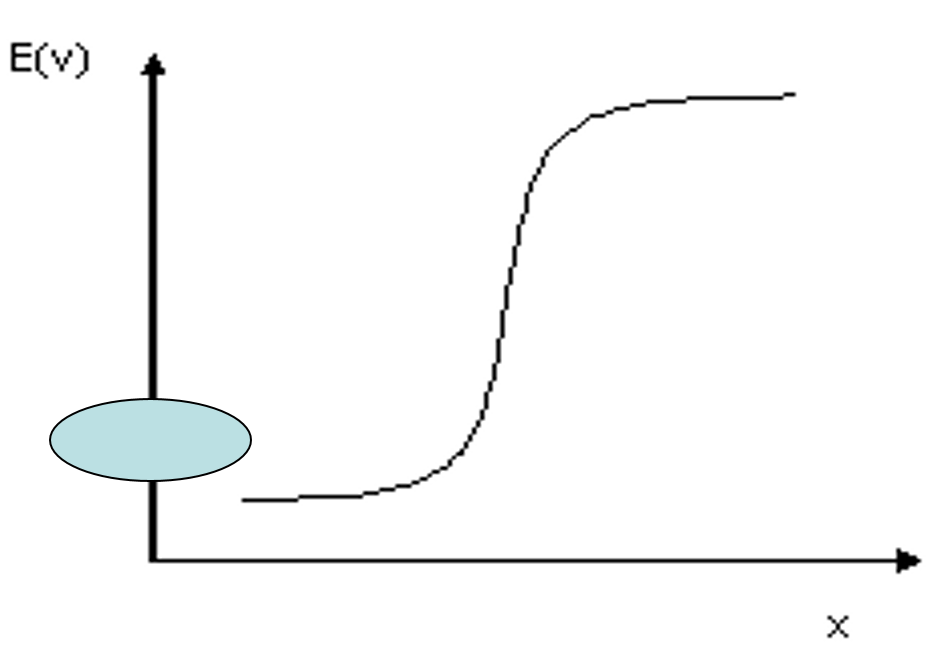
Interprétation

D’après l’équation (\ref{avant_eq}), E mesuré E_m sera d’autant plus faible que la [Cl^–] est plus élevée. Au fur et à mesure de l’ajout de AgNO₃,E_m augmente lentement et lorsque tous les Cl^– sont consommés sous forme de AgCl , on observe un saut brusque de Em qui indique le point équivalent équation ( \ref{a_equi}). Un excès de Ag⁺ engendre un Em proportionnel à [Ag⁺]. Celui ci augmente lentement à nouveau au cours de l’addition du réactif titré (équation \ref{apres_eq}).

Remarques :

• Au temps t₀, E est mal défini, pas de Ag⁺ dans le milieu.
• A x =1: E mesuré est constant et ne dépend que du Ps
• Au delà du point équivalent, on peut négliger Ag⁺ provenant de la dissolution de AgCl devant l’excès du réactif.
• les points à 0,1 % près de part et d’autre de l’équivalence déterminent le saut potentiométrique donc la précision du dosage.

Dosage d’un mélange d’halogénures (Cl^– et I^–):

Dès l’ajout du réactif (Ag⁺), AgI précipite en premier (précipité moins soluble).
Dans cet exemple, on a 2 points équivalents, Le 1er correspond aux {I^-} et le second aux Cl^–.
\begin{align} AgCl &\rightleftharpoons Ag^+ + Cl^- &Ps_1 &= 10^{-10}\\ AgI &\rightleftharpoons Ag^+ + I^- &Ps_2 &= 10^{-16} \end{align}
La détermination des équations du E au cours du dosage est analogue à celle de l’exemple précédent, on retrouve les mêmes expressions.

Allure de E_m = f(x), 2 sauts potentiométriques.

NB: on peut traiter ces titrages non pas en fonction de x (fraction molaire) du réactif ajouté, mais en fonction des volumes.

Représentation des courbes de titrage par des diagrammes logarithmiques

Influence des valeurs des Ps

Soit :
\begin{align}
[AgI] \;Ps_1 = 10^{-16} \qquad [AgBr] Ps_2 = 10^{-12} \qquad [AgCl] Ps_3 = 10^{-10}
\end{align}

On trace sur la même courbe pour les trois composés

• E = f(x) pour : X= 0; 0,5; 1,0; 1,5; 2,0
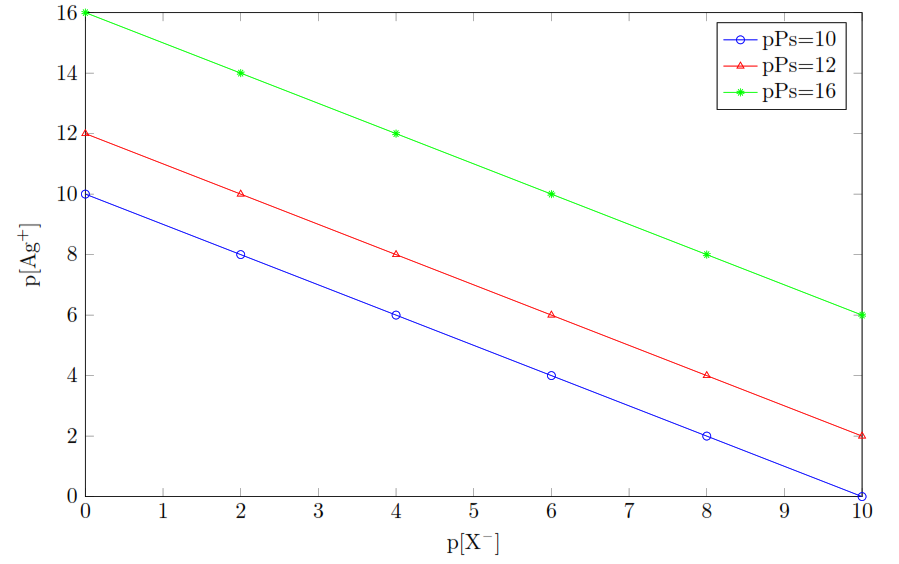
• Puis p(Ag⁺) = f(p X^–): pX^– = 0; 2; 4; 6; 8;10; 12

Tracé des courbes

Diagramme E = f(x)

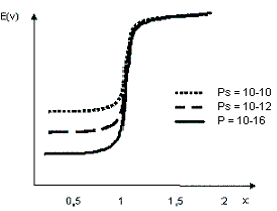
On constate que plus le Ps est faible, plus le saut potentiométrique est élevé, et plus la précision est meilleure.

Diagrammes logarithmiques :

Soit l’équilibre:
\begin{align} A_mB_n &\rightleftharpoons mA + nB & Ps &= [A]^m\cdot[B]^n\\ \log[B] &= \dfrac{\log(Ps)}{n} – \dfrac{m \cdot \log[A]}{n}\\ p[B] &= \dfrac{p(Ps)}{n} – \dfrac{m\cdot p[A]}{n} \end{align}

• Tracer : p(B) = f(pX),
• par exemple Hg₂Cl₂, AgCl et PbCl₂
• Quand p(B) = 0: l’ordonnée à l’origine = 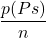\dfrac{p(Ps)}{n} et la pente de la droite est \dfrac{m}{n} .

Exploitation

Déterminer:

• p[Cl^–] pour une précipitation quantitative de Ag⁺ à partir d’une solution 0,1M.
• la fraction de Hg₂²⁺, Ag⁺ et Pb²⁺ restant non précipité à [Cl^–] = 1, pour une concentration métallique 0,1M.

Influence de la concentration initiale C₀

Soit le composé AgI de Ps = 10^-16

• C0₁= 10^-2 p[C0₁] = 2
• C0₂ = 10^-4 p[C0₂] = 4

Tracé des courbes potentiométriques :

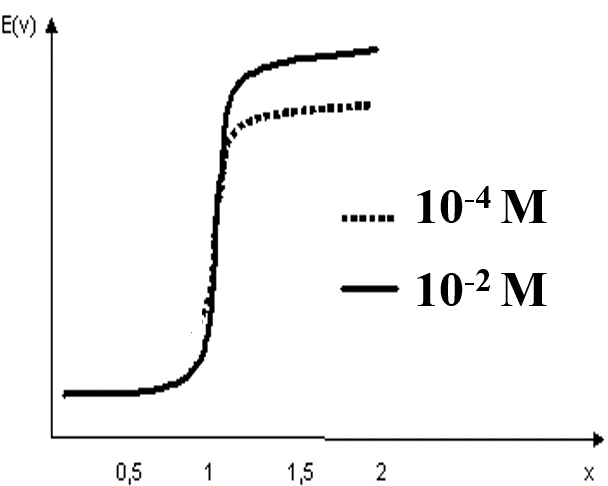
On constate que le saut potentiométrique le plus faible correspond à la solution diluée. La précision sur le dosage sera moins bonne.

Applications de l’argentimétrie

• Méthode de Mohr: Cl^–, Br^– (NH₄⁺); Cl^–, Br^–, I^–(K+); CaBr₂, SrBr₂ ; Cl^– acétylcholine …
• Méthode de Charpentier-Volhard:
  • Cl^–(histamine, histidine , lysine, procainamide, thiamine…)
  • Br^–(penta et hexaméthonium);
  • CN^– (eau de laurier-cerise); Théophylline et dérivés; acide urique et acides organiques;
  • Cl^– (chloramphénicol, cystéine)
  • S (de dérivés organiques)
  • Colloïdes d’Argent; Bromure de tribromoéthanol.
• Paneth-Fajans: Tous les dosages précédents sont réalisés.

[WpProQuiz 8]

Pages : 1 2