Méthodes d’extraction

Extraction Liquide – Liquide

Introduction

L’extraction Liquide – Liquide est basée sur les différences de solubilité des substances dans deux solvants non miscibles: celui qui contient le soluté (noté A) et le solvant d’extraction (noté B). A l’équilibre, lorsque le soluté est distribué entre les deux liquides, il se réalise une extraction simple dite unique ou à multiple dite n étages. En général, un des solvants est l’eau, l’autre est un solvant organique non miscible: le toluène, CCl₄ , CHCl₃, l’ether-diéthyle.

---

Extraction simple

Principe

Une extraction simple ou une extraction à un étage est réalisée par mise en contact de la solution du soluté avec un certain volume d’un solvant non miscible, agitation vigoureuse et décantation des deux phases liquides en ampoule à décanter ou par centrifugeuse pour séparer les deux phases liquides non miscibles.

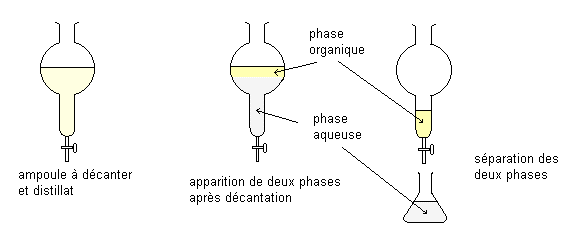
• Le solvant B, après extraction, s’appelle l’extrait ou la couche extraite.
• Le solvant A, après extraction, s’appelle le raffinat ou la couche raffinée.

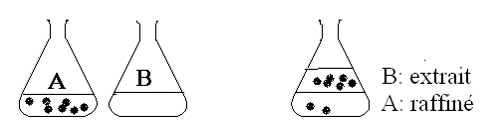
Aspects quantitatifs

• Cas d’une distribution régulière

On entend par distribution régulière, le partage du soluté dans les deux phases liquides non miscibles, quelle que soit sa concentration initiale et dans les conditions suivantes:

• non miscibilité absolue des solvants
• pas d’interaction entre le composé et le solvant
• même état physique pour le soluté et le solvant

Coefficient de partage

Un soluté X est dissout dans un solvant A (en général de l’eau) auquel, on ajoute un solvant B non miscible (organique) puis on agite. Le soluté X se répartit entre le solvant A et le solvant B. A l’équilibre on a toujours un rapport de concentrations constant. Ce rapport est le coefficient de partage .

\begin{align}\lambda = \frac{C_B}{C_A}\end{align}

Soit:

Q_A0: quantité initiale de soluté dans un volume V_A de solvant A
Après mise en contact et agitation de cette solution en présence d’un volume V_B de solvant B, non miscible au premier et de polarité plus faible, on a un équilibre tel que le soluté se répartit entre les deux solvants:

\begin{align}Q_{A0} &= Q_A + Q_B\\ \lambda &= \frac{C_B}{C_A} \end{align}

où : et

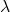• est constant pour une température donnée, un soluté et deux solvants donnés
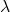• est constant dans le cas d’une distribution régulière.
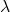• est aussi égale au rapport des solubilités du soluté dans les solvants B et A

Loi de Berthelot – Iungfleisch:

Quelle que soit la valeur de la solubilité d’un corps à partager entre deux solvants non miscibles et quels que soient les volumes de ces solvants, le corps se répartit de telle sorte qu’à l’équilibre les concentrations sont dans un rapport constant.

Coefficient de partage corrigé

ou rapport de quantités

\begin{align}\alpha &= \dfrac{Q_B}{Q_A}\\ \alpha &= \dfrac{C_B}{C_A}\times \dfrac{V_B}{V_A} = \lambda \cdot \dfrac{V_B}{V_A} \end{align}

Si le volume varie, varie

Rendement

Le rendement R d’une extraction simple est défini par:

avec:

• Q_A0 = quantité initiale du soluté dans le solvant A.
• Q_B = quantité initiale du soluté dans le solvant B.

\begin{align} R &= \dfrac{Q_B}{Q_{A0}} \\ \alpha &= \frac{Q_{B1}}{Q_{A1}} = \lambda \cdot \dfrac{V_B}{V_A}\\ Q_{A0} &= Q_{B1} + Q_{A1} \qquad Q_{A1} = \frac{Q_{B1}}{\alpha}\\ Q_{A0} &= Q_{B1} + \frac{Q_{B1}}{\alpha} = Q_{B1} \cdot(1 + \frac{1}{\alpha})\\ Q_{B1} &= Q_{A0} \cdot (\frac{\alpha}{1 + \alpha}) \Rightarrow R = \dfrac{\alpha}{1 + \alpha}= 1 – \dfrac{1}{(1 + \alpha)}\\ \text{Ou :} Q_{A0} &= Q_{A1} + \alpha \cdot Q_{A1} = Q_{A1} (1 + \alpha) \\ Q_{A1} &= \frac{Q_{A0}}{1 + \alpha} \qquad Q_{B1} = Q_{A0} – Q_{A1}\\ \text{D’où : } R &= \dfrac{\dfrac{Q_{A0} – Q_{A0}}{(1 + \alpha)}}{Q_{A0}} \Rightarrow R = 1 – \dfrac{1}{(1 + \alpha)} \end{align}

Le rapport montre que quelle que soit la valeur de [/latex]\alpha[/latex], le rendement est toujours inférieur à 1 (<100%).

exercice

quiz ici

Représentation graphique de la distribution régulière

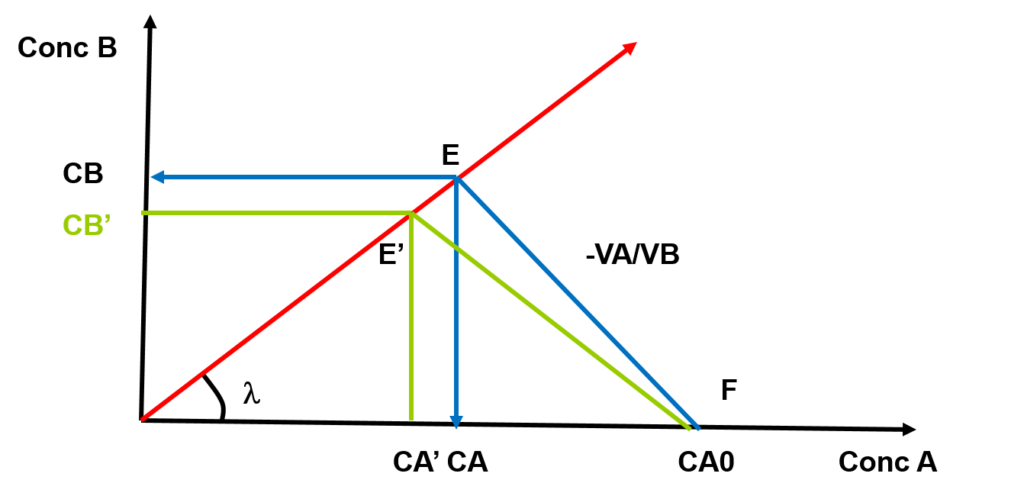
• Interprétation: pour une concentration initiale C_A0
  • un coefficient de partage
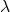
  • un choix de volumes de phases V_A et V_B
    seront obtenues les concentrations C_B dans l’extrait et C_A dans le raffinat.
    Une augmentation du volume V_B par rapport à V_A permet de diminuer la pente du segment EF à E’F et donc de minimiser la concentration résiduelle C_A à C_A’ du soluté dans la phase A. De ce fait C_B diminue C_B’ aussi, mais seulement par augmentation du volume V_B.
• Conclusion: Le choix du solvant d’extraction et de son volume V_B sont des facteurs essentiels car ils conditionnent la valeur du coefficient de partage 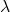ainsi que le rendement d’extraction

(1)  

---

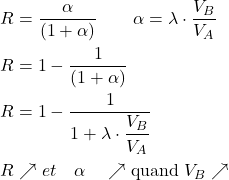
Extractions répétées

L’objectif est d’extraire le maximum de composants (être le plus près possible de 100 %)

Principe

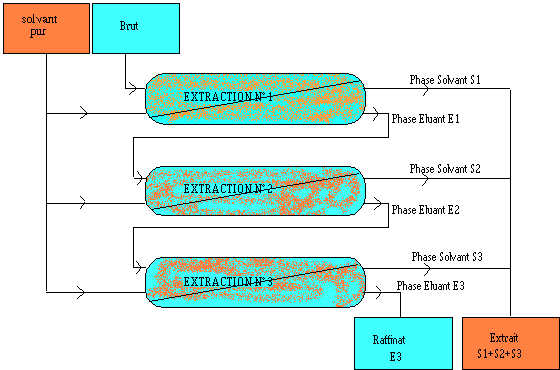
On répète les extractions sur la solution aqueuse de départ, on parle d’extraction à plusieurs étages.

Aspects quantitatifs

Cas de distribution régulière

• 1er étage: On prend un volume de solvant A avec une quantité Q_A0 du composé à extraire, puis on ajout d’un volume du solvant B pur, après agitation vigoureuse (équilibre de répartition). On recueille le solvant B contenant la quantité Q_B1 du composé à extraire ; il reste une quantité Q_A1 dans le solvant A.
• 2ème étage: On ajoute un volume V_B du solvant B pur. Nouvelle extraction; recueil du solvant B contenant la quantité Q_B2 et on le joint au volume déjà extrait; il reste Q_A2 dans le solvant A.
• n^ème étage: On continue de même jusqu’au n[/latex]^{ème}[/latex] étage: à l’étage n on a la quantité Q_Bn dans le solvant B. Il reste Q_An dans le solvant A.

Expression des quantités de soluté distribuées:

(2)  

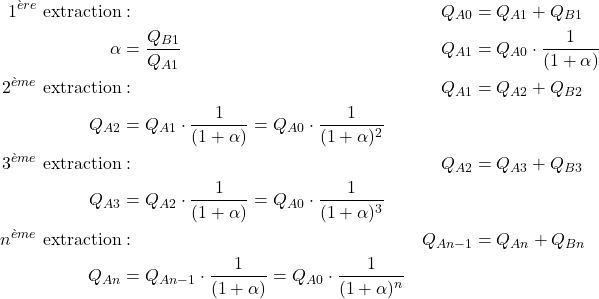
Rendement global :

-pour 3 étages

(3)  

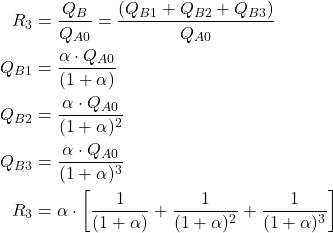
-Pour n étages En général, on utilise un volume de solvant V_B identique:

(4)  

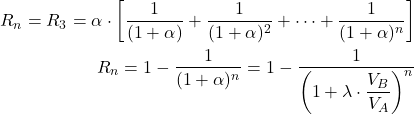
Optimisation

• Si V_B important : l’évaporation prend plus de temps et d’énergie
• Si n est important : temps important

On cherche le meilleur compromis
(V_B: Volume total de B et V_b: Volume de B ajouté à chaque étage)

(5)  

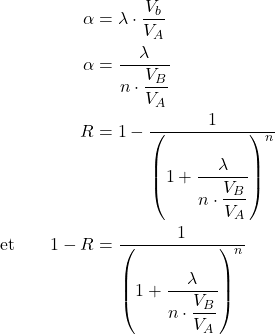
Utilisation des abaques

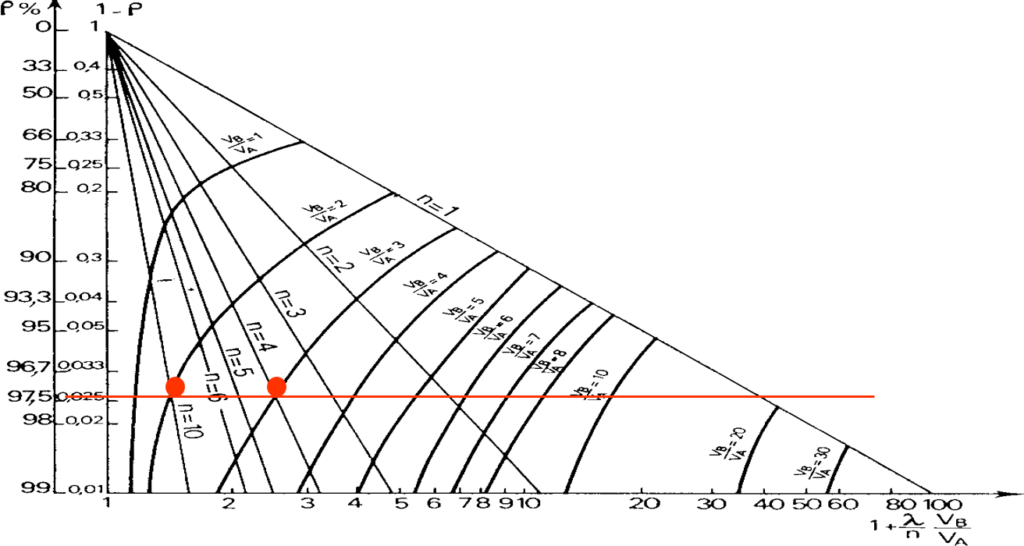
(6)  

Deux variables:
Le nombre d’étage n et le volume V_B}

• Si on fixe n : 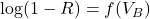: on obtient les courbes (\dfrac{V_B}{V_A})
• Si on fixe V_B: 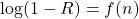: droite de pente – n

Aux intersections des courbes n et V_B connus, R est déterminé.

exercice

Déterminer le rendement en choisissant le volume et le nombre d’étages :

(7)  

Le coefficient de partage d’une substance neutre est de 5, Calculer le rendement d’extraction :

1. Lorsque 30 ml d’éther est ajoutée à 10ml d’eau?
2. Lorsque 3 extractions successives de 10 ml d’ether ajoutés à 10ml d’eau?

Cas d’une distribution irrégulière

Coefficient de distribution

Si on est dans des conditions non idéales, le rapport entre les concentrations totales du soluté sous quel qu’état qu’il se trouve est le coefficient de distribution.

(8)  

Représentation graphique de la distribution irrégulière:

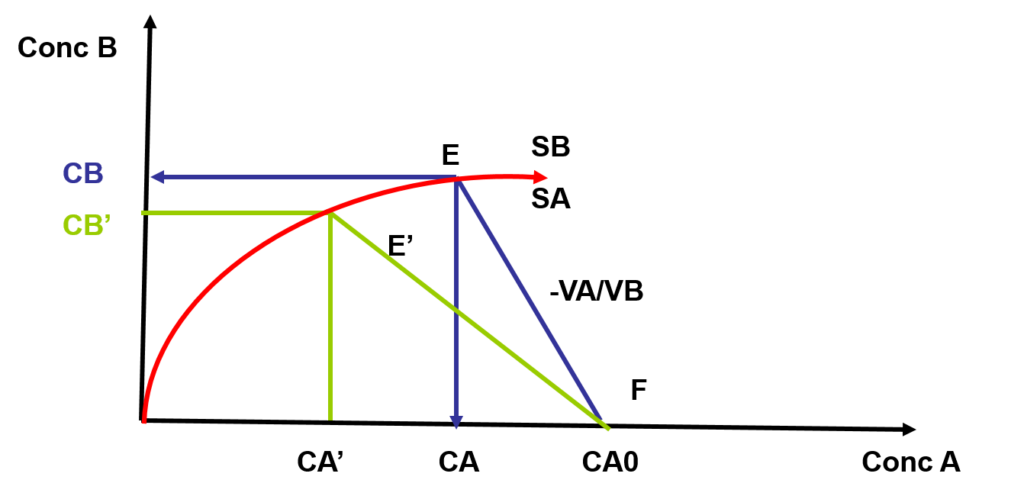
Le taux de distribution n’est pas constant.

De la même manière que pour la distribution régulière, une augmentation de V_B améliore le rendement d’extraction.

Applications

Elle intéresse les molécules organiques et minérales, on peut extraire une molécule à partir d’un milieu biologique, extraire une molécule à partir d’un médicaments à doser…

L’extraction a 2 objectifs :

• Purifier: élimination des composés pouvant gêner l’analyse
• Concentrer le soluté par exemple l’analyse des métaux à l’état de traces dans l’eau « concentration 1000 fois ».

Composés minéraux

Ils sont très difficilement solubles dans les solvants organiques:
[/latex]\Rightarrow[/latex] ne sont pas extractibles par un solvant organique sauf s’ils présentent des liaisons covalentes ou de coordination (organométalliques).
Exemple :

• acide diméthylarsénique,
• complexes (chlorure mercurique)

Molécules organiques

Leur solubilité en solvant organique dépend de  :

1. la longueur de la chaîne carbonée, le coefficient de partage augmente quand la chaîne carbonée augmente (de 4 unités quand on ajoute un CH₂ à la chaîne carbonée).
2. la présence de groupements ionisés/ionisables.
3. la géométrie: un composé ramifié a un coefficient de partage plus faible que son isomère linéaire.
4. Un composé insaturé a un coefficient de partage plus faible que le composé saturé.
5. les hétéro-atomes N, O, S: diminuent le coefficient de partage
6. les halogènes : augmentent le coefficient de partage

Exemples d’Applications:

Exemples d’extraction des acides et des bases

acides:

(9)  

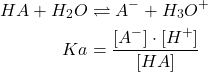
Seules les molécules HA passent en phase organique avec:

Un coefficient de partage:

(10)  

Un coefficient de distribution :

(11)  

En tenant compte des 3 relations précédentes:

(12)  

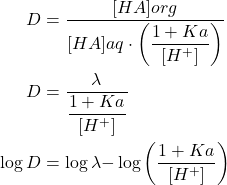
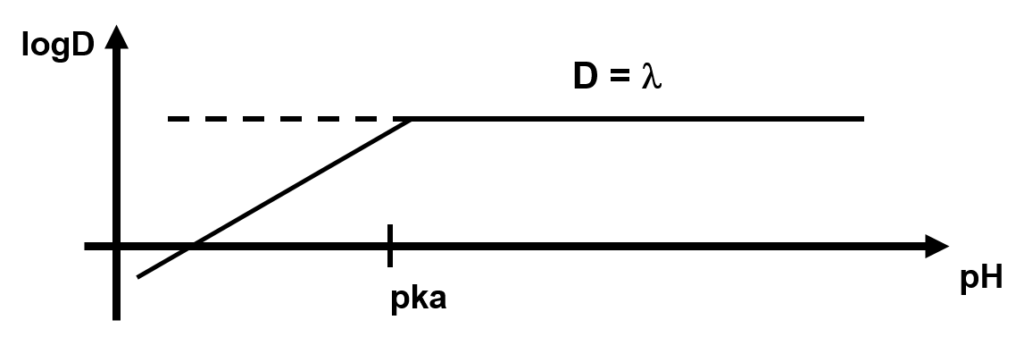
En fonction de la valeur de

Si le pH est bas :

Si le pH est élevé :

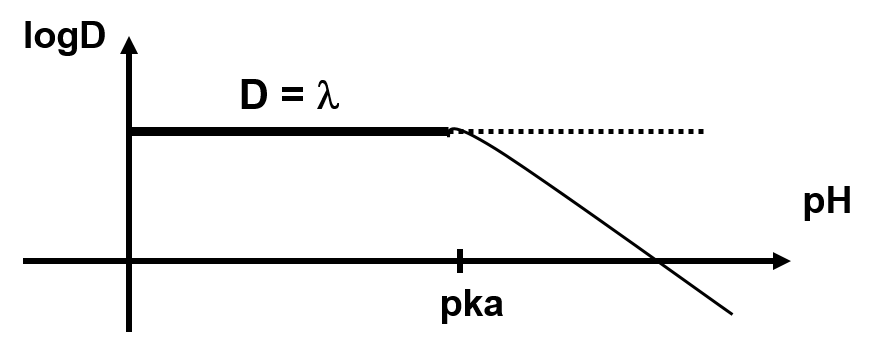
Pour extraire l’acide, il faut se trouver à pH < pKa , en général pH = pKa – 2)

Une solution de formule pharmaceutique suivante:

• Base A pka 6,7:
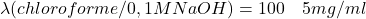
• Base B pka 9,7:
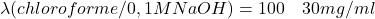
• Acide benzoique pka 4,2:

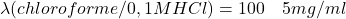
Pour extraire sélectivement la base A, 5ml de la solution est mélangé avec un tampon phosphate pH 6,7 Puis suivi d’une extraction avec 60 ml de chloroforme

Calculer le rendement et la masse de chaque composé extrait ?

Pour les acides:

(13)  

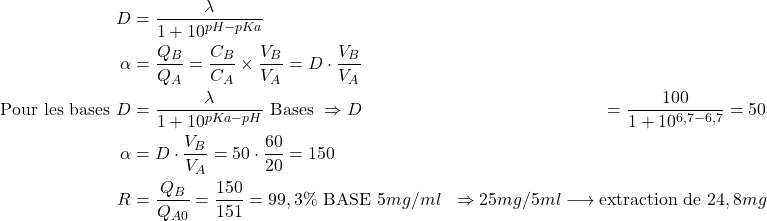
bases :

(14)  

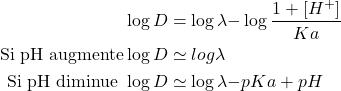
Se placer à pH > pKa pour extraire les bases
(pH> pKa + 2 mais pas trop)

Exemples d’extraction des Chélates métalliques

Principe :
On met à profit la formation de complexes pour extraire des métaux.

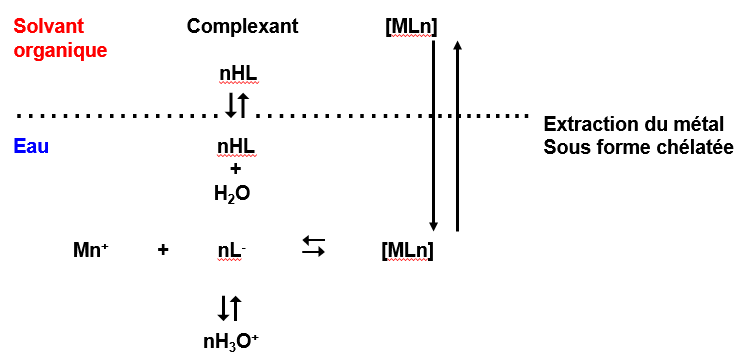
Les chélates sont importants au point de vue analytique, les équilibres qui interviennent sont les suivants :

(15)  

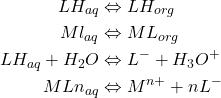
L: Ligand ,agent complexant \qquad M: Métal

• Constante de partage :
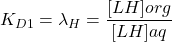
• Constante de partage : [/latex]K_{D2} = \lambda_M = \dfrac{[ML]{org}}{[ML]{aq}}[/latex]
• Constante d’acidité :
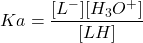
• Constante de stabilité :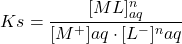

on introduit E_ML(constante d’extraction du complexe)

(16)  

Taux de distribution:

Ce qui intéresse l’analyste c’est l’extraction du métal avec un bon rendement.

(17)  

l’expression de D, en fonction des diverses constantes (K_D1 K_D2 Ka Ks ):

(18)  

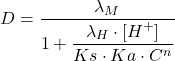
avec:

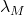• : coefficient de partage du métal (complexe dans phase organique/aqueuse)
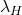• : coefficient de partage de l’agent complexant
• Ks : constante de stabilité du complexe
• Ka : constante d’acidité de l’agent complexant
• C : concentration de l’agent complexant
• n : nombre de coordinats

Rendement

(19)  

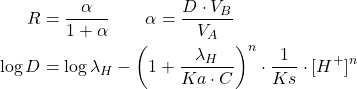
Facteurs d’influence sur l’extraction

(20)  

dans cette expression trois termes interviennent sur le taux de distribution (D) :

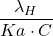1. : Correspond au réactif (chélateur).
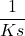2.   : Concerne le complexe ou chélate, donc la nature de M. 
3. [H₃O⁺]: Fait intervenir le pH du milieu.

• Mise en oeuvre

Chélateurs	Chélateurs
diphénylthiocarbazone	CCl4
Dithiazone	CHCl3
pyrolidine dithiocarbamate	Cétones

Exemples d’extraction de paires d’ions

Il s’agit d’une association de 2 ions de signe contraire. Cette association existe dans des solvants peu dissociant et la paire d’ion s’y comporte comme une molécule neutre. Il est alors possible d’extraire la paire d’ions.
On a toujours l’équilibre suivant 

(21)  

Constante de stabilité de la paire d’ions:

(22)  

La paire d’ions est d’autant plus stable que la constante diélectrique est plus faible.

Extraction:

(23)  

Constante de partage

\begin{align}K_D= \dfrac{(A^-,BH^+){org}}{(A^-,BH^+){aq}}\end{align}

\begin{align}: (A^-){aq} (BH^+){aq}\Leftrightarrow (A^-,BH^+)_{org}\end{align}

Taux de distribution :
La concentration de la paire d’ions dans le solvant eau est peu stable. On peut la négliger.

\begin{align}D &= \dfrac{[A^-,BH^+]{org}}{[BH^+]{aq}} \\D &= \dfrac{[(A^-,BH^+){org}]\cdot K\cdot [A^-]{aq}}{ (A^-,BH^+){aq}} \\ D &= K_D\cdot K\cdot [A^-]{aq}\end{align}

Différents types de paire d’ions extractibles:
Pour une extraction quantitative, il est parfois suffisant que l’un seulement des deux ions soit volumineux et hydrophobe.

1) Anions :

• Tensioactifs anioniques
  • Sulfate acide d’alcoyle : exemple laurylsulfate de sodium (dodécylsulfate) C₁₂H₂₅OSO₃Na
  • Sulfonate d’alcoyle: exemple dioctylsulfosuccinate de sodium (DOSS)
• Tétraphényl borate
• Anions de colorants acides dérivés de phtaléines :
  • fluorescéines :eosinate (tétrabromofluorescéinate) ; 
  • sulfone phtaléines. 
• Anions d’ampholytes comme l’héliantine sous leur forme basique.

2) Cations:

Ce sont des dérivés azotés, il s’agit le plus souvant d’ions ammonium tertiaire ou quaternaire à caractère hydrophobe suffisant.

• Ammoniums quaternaires à longue chaine, les associations comportant par exemple les ions cétyltriméthylammonium, cétylpyridinium, benzyltrialkylammonium sont aisément extraites en phase choloroformique ou benzénique.
• Dérivés d’amines de masse moléculaire élevée dioctylsulfosuccinate de quinine

Pages : 1 2 3 4