Généralités sur l’électrochimie

Théories simplifiées de l’électrolyse

• Échange des e-
• Déplacement des ions
• Prévision des réactions \rightarrow E équilibre \rightarrow E équilibre

Potentiel d’équilibre (E. rédox, E. électrode)

Soit une solution d’un système Redox

\begin{align}Ox + e- \rightarrow Red\\
Red – e- \rightarrow Ox \end{align}

un fil conducteur en platine (Pt)
L’échange d’e- entre Pt et Ox ou Red il s’établit un équilibre.

La composition de la solution est constante au voisinage de l’électrode.
L’électrode de Pt prend un potentiel E d’équilibre (Nernst):

E = E^0 + \dfrac{RT}{nF} .\log \dfrac{Ox}{Red}

Ex. Fe³⁺/Fe²⁺ ; CuSO₄/Cu

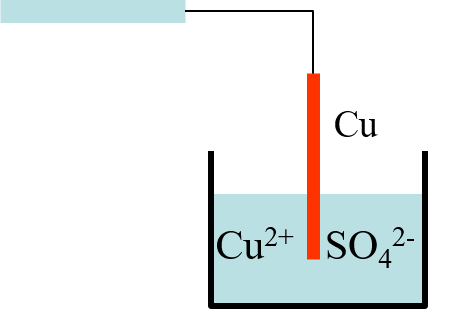
Potentiel de l’électrode: Cu²⁺/Cu:

• Réduction: e- pris au Cu qui se charge (+). La solution perd Cu²⁺ se charge (-). Le Cu attire les SO₄^2-. Apparition d’une double couche et donc un champ électrique s’opposant à la réduction.
• Oxydation: le cuivre metal Cu libère des e-; le métal se charge (-) ; la solution gagne des Cu²⁺ se charge (+) d’où un champ électrique.

Dans les deux cas, il apparaît un potentiel E entre le Métal et la Solution:
E = V_M-V_S (différence de potentiel interfaciale)

Pile électrochimique (2 demi-réactions ):

2 électrodes plongeant dans 2 solutions de M1 (n1+) et M2 (n2+) séparées et reliées par un pont salin ou membrane:

\begin{align} E_1 = V_{M1}-V_{S1} \text{ et } E_2 = V_{M2}-V_{S2}: \end{align}

Le pont impose l’égalité V_S1 = V_S2
La différence de potentiel (ddp) observée est : E = V_M1-V_M2 = E_i= E₁– E₂ (Voltmètre)

• Équimolaire \Longrightarrow rien
• E_i > E \Longrightarrow Oxydation
• E_i < E \Longrightarrow Réduction

Principe de l’électrolyse

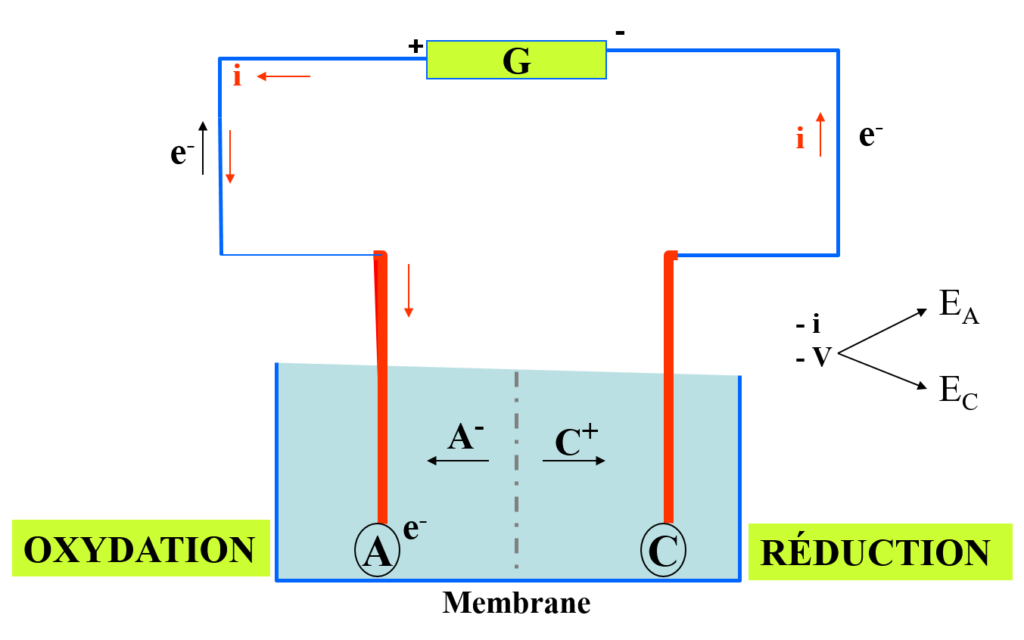
https://media.pearsoncmg.com/bc/bc_0media_chem/chem_sim/html5/Electro/Electro.php

Ex. CuCl₂

\begin{align} \text{A :}\qquad & Cl- \rightleftharpoons \dfrac{1}{2}Cl_2 + e^- &\Rightarrow E_{Cl} = E^0 + ….\\ \text{ C :} \qquad &\dfrac{1}{2}Cu^{2+} + e^- \rightleftharpoons \dfrac{1}{2}Cu &\Rightarrow E_{Cu} = E^0 + …. \end{align}

Conditions de l’électrolyse:

\begin{align}  E_A - E_C > E_{Cl} - E_C \text{Ou} E_C < E_{Cu} \Rightarrow E_A - E_C > E_{Cl} - E_{Cu} \text{Condition de l’électrolyse}  \end{align}

NB: l’échange d’e- peut être lent.

Potentiel imposé à G : \delta E = V = E_A - E_C

Prévisions des réactions

Règles :

• Substances oxydables ANODE
• Substances réductibles CATHODE. (Remarque: la charge n’intervient pas)
• Substance à E (-) élevé s’oxyde en premier
• Substance à E (+) élevé est réduite en premier

Ex. CuSO₄ (0.1M) en milieu H₂SO₄ (M/2)
Oxydations possibles:

Réductions possibles:

\begin{align} Cu^{2+} +2 e^- &\rightleftharpoons Cuo \qquad E = 0.34 + \dfrac{0.06}{2} log [Cu^{2+}] = 0.31V \\  2H^+ +2 e^- &\rightleftharpoons H_2 \qquad E = E^0 = 0 \end{align}

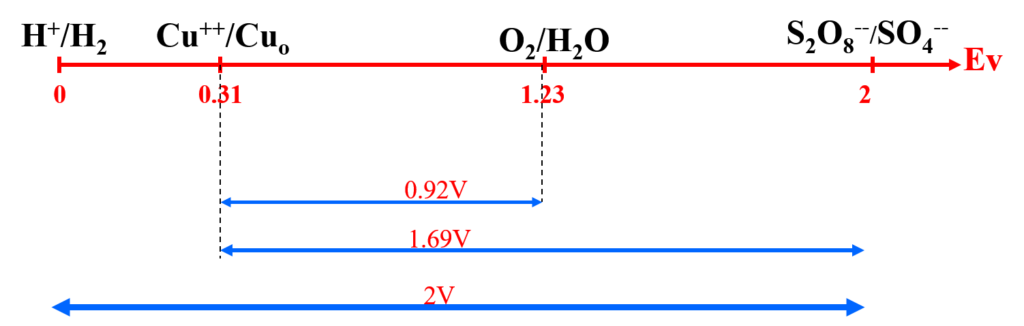
1. Chercher la ddp à appliquer (Conditions d’électrolyse)
2. Appliquer les règles

• C1 : réduction Cu²⁺
• A1 :oxydation H₂O
• C1 : réduction Cu²⁺
• A1 : oxydation H₂O

électrolyse a lieu si :
E_A1– E_C1 > 0.92 ; E_A> 1.23 et E_C < 0.31

Remarques:

1. Cette condition est nécessaire mais non suffisante car l’échange des e- peut être infiniment lent. C’est ce que nous examinons dans la seconde partie
2. les substances qui disparaissent (par électrolyse) :
    dissoutes: ions ; molécules ou M de l’électrode  M+
   solvant: H2O \textrightarrow O2 \\ \textrightarrow H2

Les substances qui apparaissent : gaz ou précipité, si M₀, il recouvre l’électrode.
Quand une substance participe aux réactions d’électrolyse sa concentration diminue.

Ex. Ag⁺ (E⁰ = 0,8 V) est réduit avant Cu²⁺.
Question: Quand démarre la réduction de Cu²⁺?
Réponse: E_éq (Ag⁺) devient < E_éq (Cu²⁺)

Les substances qui se forment à l’anode par oxydation peuvent passer en solution et être réduites à la cathode. => membrane

Théories I = f(E)

Première hypothèse : vitesse d’échangés des électrons finie (i ≡ nombre d’électrons)

Oxydant ou Réducteur seul

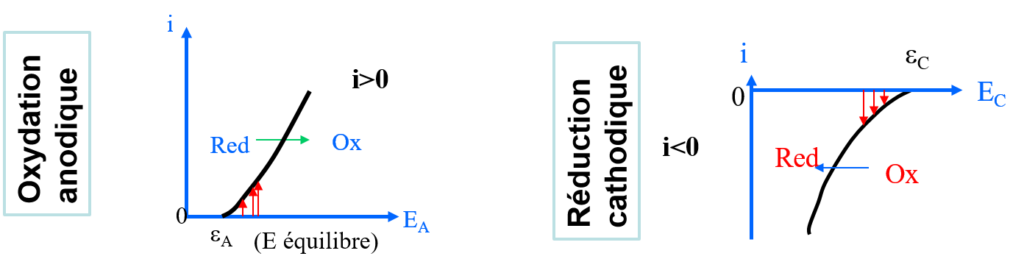
Oxydant et réducteur d’un même couple

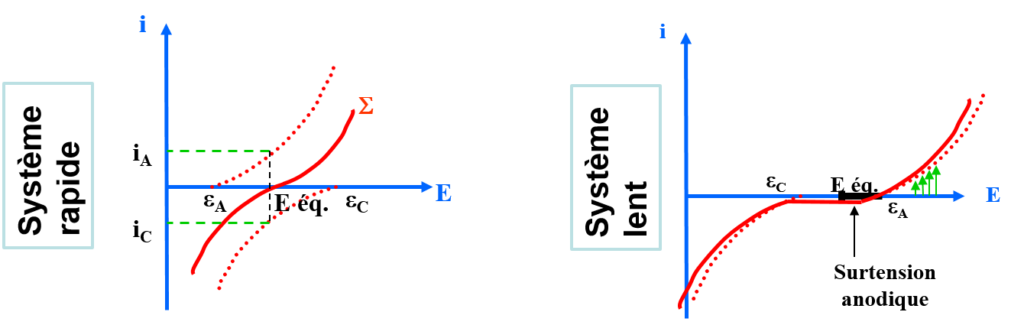
Prévision des réactions

I = f (E) connues
Ex : solution acide Fe³⁺, S₂O₈^2- ; (Électrode graphite)

Oxydation : H₂O/O₂ , E° = 1,33 V + sur-tention = 2,83 V

Réduction :

gggggg

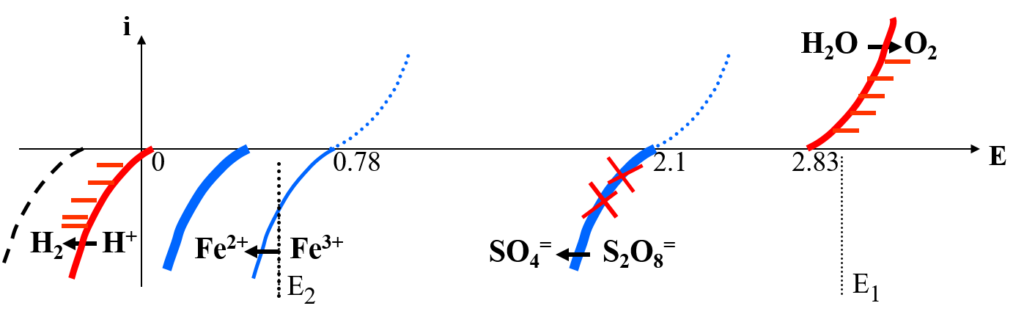
SV : → mur (domaine)
(X) : non électroactive
Appliquer E₁E₂ : Fe³⁺ à Fe²⁺ ?

Théorie tenant compte des phénomènes de transport

Généralités

Vitesse de transport en solution  finie

On distingue 3 modes de transport de matière en solution:

• Migration i_m: déplacement des ions sous l’effet du champ électrique dans un gradient de potentiel électrique.
• Diffusion i_d : déplacement de matière des milieux les plus concentrés vers les moins concentrés. La diffusion est le déplacement sous l’effet d’un gradient de potentiel chimique.
• Convection i_c: les déplacements dus à des phénomènes autres que la migration et le diffusion sont rangés sous le nom de convection. ils peuvent être dus à un gradient de température, de pression… L’agitation mécanique de la solution est le plus important.

Migration

• Influence de E sur les ions
• n e- échangés à la surface de l’électrode
• n charges passent dans la solution

Diffusion

Variation de la concentration au voisinage d’électrode à gradient de concentration

Convection

Autres causes de déplacement ; T°, vibration, densité, agitation…
i_éle = i_m + i_d + i_c

Courant de diffusion

Nernst : hypothèse : diffusion limitée à une couche d’épaisseur \Delta x autour de l’électrode

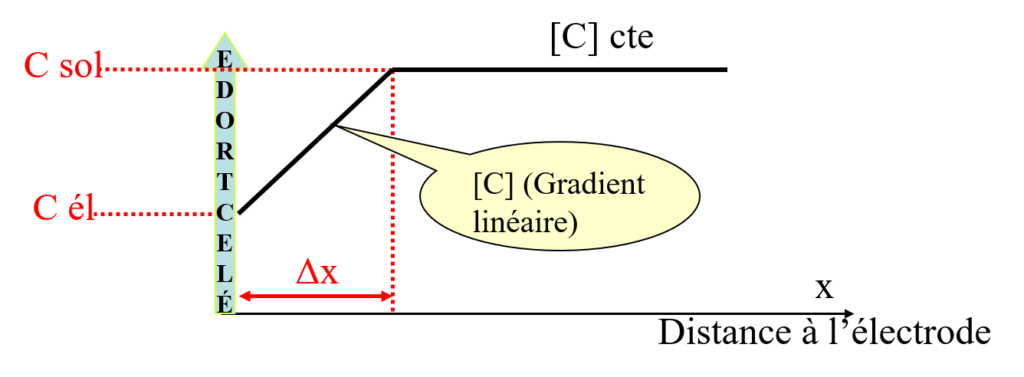
Loi de Fick : vitesse de transport par diffusion \equiv au gradient linéaire de concentration.

!!!!!!dxdt=SD⋅(Cs−Cel)Δx \\

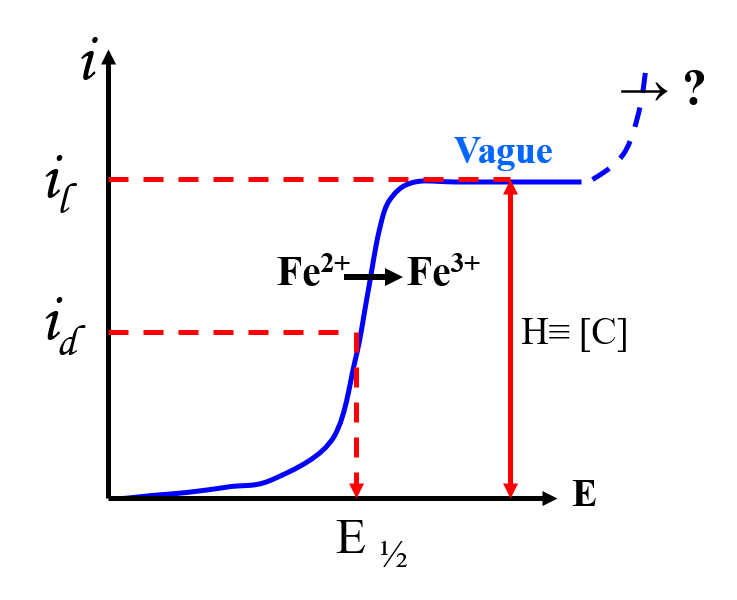
Allures des courbes

\begin{align} id &= K Fe^{2+} [Fe^{2+}s – Fe^{2+}{el}]\\
Fe^{2+}_{el}& \longrightarrow 0 \qquad \qquad i_d \longrightarrow i_l\\
i_l &= K Fe^{2+} [Fe^{2+}]_s \text{ mesure sur pallier}
\end{align}

Domaine d’électroactivité

Étude :

1. Tracer le mur
2. Choix du solvant, d’électrode

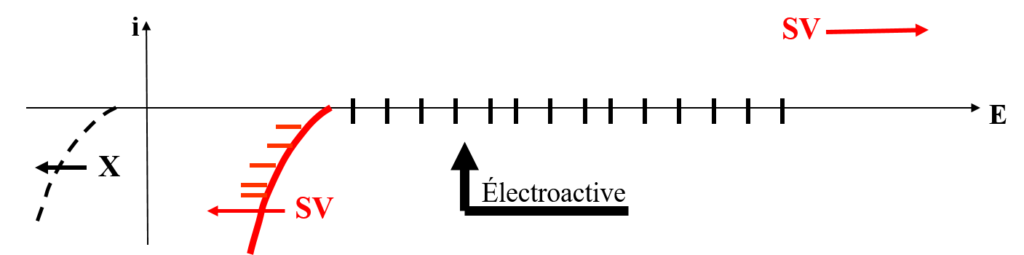
Exemple. CH₃CN augmente le domaine/ H₂O

Additivité des (i )

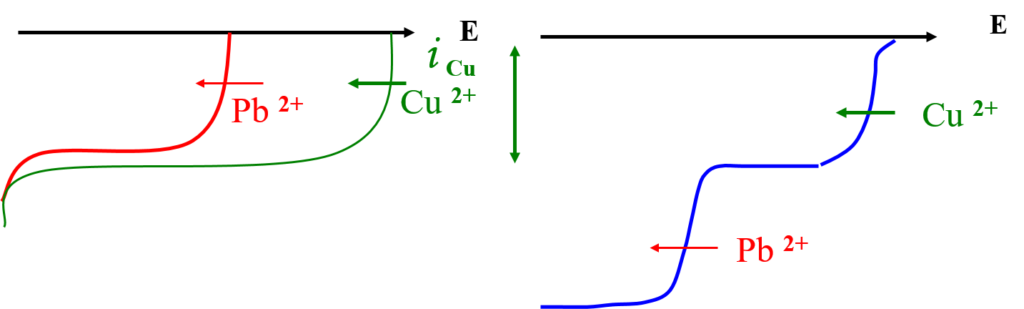
Techniques d’analyses électrochimiques

Trois composantes :
C : Concentration
E : Potentiel
I : Intensité

On fixe un paramètre et on suit la variation de l’un en fonction de l’autre.

• C fixe: i = f (E): Polarographie; Voltamètrie
• E fixe: i = f (C): Ampérométrie; Coulométrie (Coductimétrie)
• I fixe: E = f (C): Potentiométrie; Ionométrie