L’absorption et émission atomique sont deux facettes d’une même propriété énoncée par Kirchhoff  » Un corps, soumis à certaines conditions d’excitation, ne peut émettre que des radiations qu’il est susceptible d’absorber dans les mêmes conditions « .

Les techniques d’absorption et d’émission atomique sont basées sur l’absorption ou l’émission des radiations par des atomes à l’état de vapeur.

Les radiations sont du domaine de l’U.V ou du visible.

Les méthodes d’absorption et d’émission comportent 3 étapes:

1. Obtention d’atomes à l’état de vapeur = atomisation (souvent par énergie thermique).
2. Apport d’énergie à ces atomes pour les faire passer à un état excité (sous forme thermique pour l’émission atomique et sous forme de rayonnement électromagnétique pour l’absorption atomique).
3. Mesure de l’énergie.
   • Mesure de l’énergie émise : 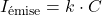(Émission atomique)
   • Mesure de l’énergie absorbée : 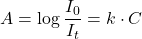(Absorption atomique)

Ces méthodes permettent:

• En émission atomique: L’identification du composé: spectre caractéristique de l’élément.
• En émission et en absorption atomique: Le dosage car l’intensité des raies absorbées ou émises est liée à la concentration de l’élément.

Structure de l’atome (rappel)

Un atome est constitué d’un noyau chargé positivement autour duquel gravitent des électrons.

A l’intérieur du noyau, on trouve des protons et des neutrons.
Le nombre de protons et d’électrons est le même = Z (numéro atomique).
Les électrons autour du noyau sont définis par les nombres quantiques

• n : nombre quantique principal:] caractérise la couche: n = 1, 2, 3,… (K, L, M,…)
• l : nombre quantique secondaire] caractérise les orbitales ou sous couches s, p, d et f:
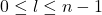
• m: nombre quantique magnétique]
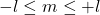
• s: nombre quantique de spin] caractérise le sens de l’orientation de l’électron

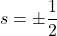
Principe de Pauli: Il ne peut exister deux électrons dont tous les nombres quantiques sont identiques

Règle simple: on a le remplissage des niveaux électroniques si le nombre quantique principal n + le nombre quantique secondaire l le plus bas : n+ l
Dans le cas n+l sont égales on commence par n le plus faible

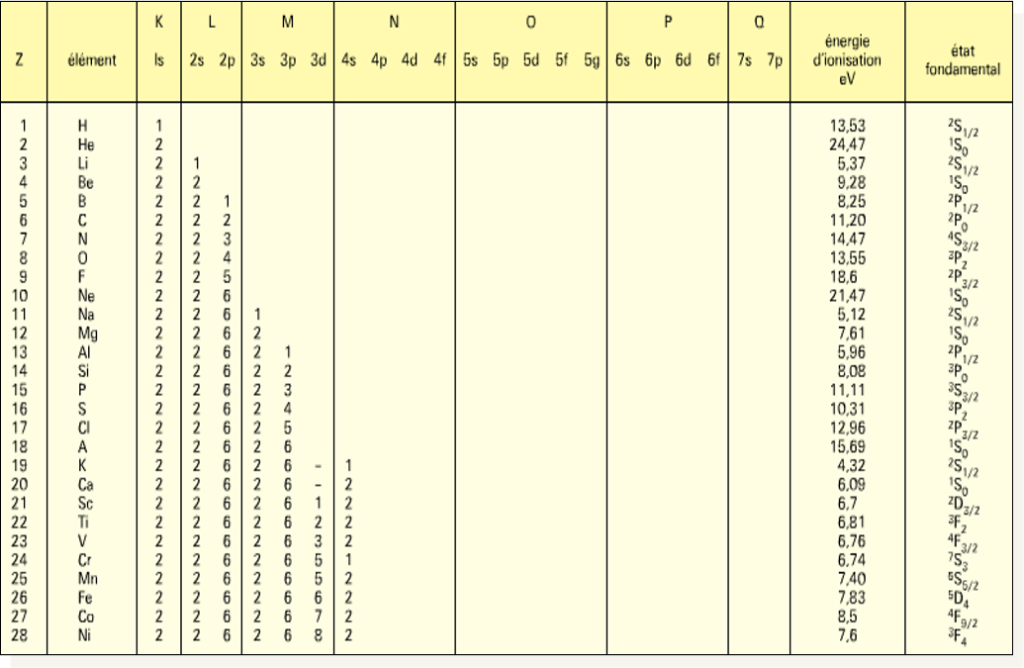
Les niveaux d’énergie

Exemple

Na:

On s’intéresse seulement aux électrons de valence donc à l’électron dans le cas de Na.

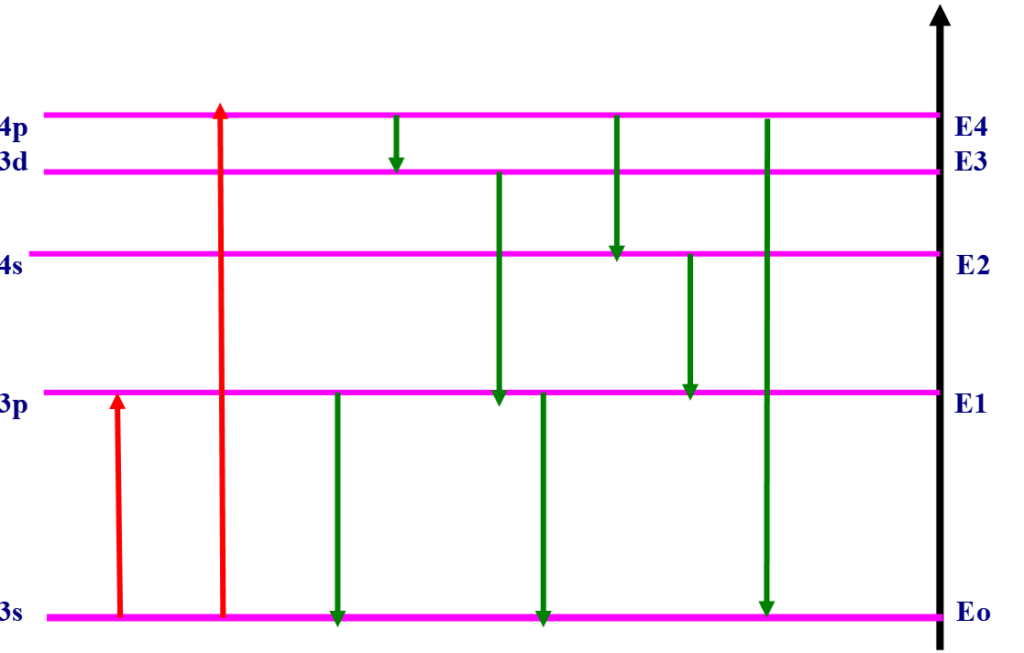
Interprétation

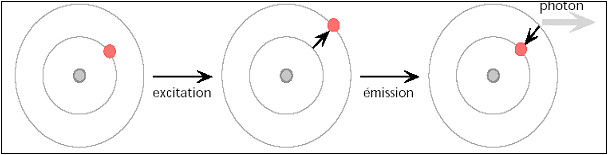
Excitation

Pour avoir une transition électronique, l’énergie d’excitation doit correspondre exactement à la différence d’énergie entre deux orbitales.

L’électron peut passer de 3s à 3p ou à 4p (la transition 3s à 4d par exemple n’est pas permise).

Règle simple: on a transition si le nombre quantique secondaire varie de ± 1:

%

$$\begin{table}[h!] % ntering % \begin{tabular}{cccc} %[/latex]{n_1s \rightarrow n_2s}& %{n_1p \rightarrow n_2p}& %{n_1d \rightarrow n_2d}& %{n_1f \rightarrow n_2f}\ %{n_2s \rightarrow n_2p}& %{n_2p \rightarrow n_2d}& %{n_2d \rightarrow n_2f}& %{n_1d \rightarrow n_2p}&[/latex] %\end{tabular} %\caption{Exemple de transition permises} %\end{table}$$

Retour à l’état fondamental

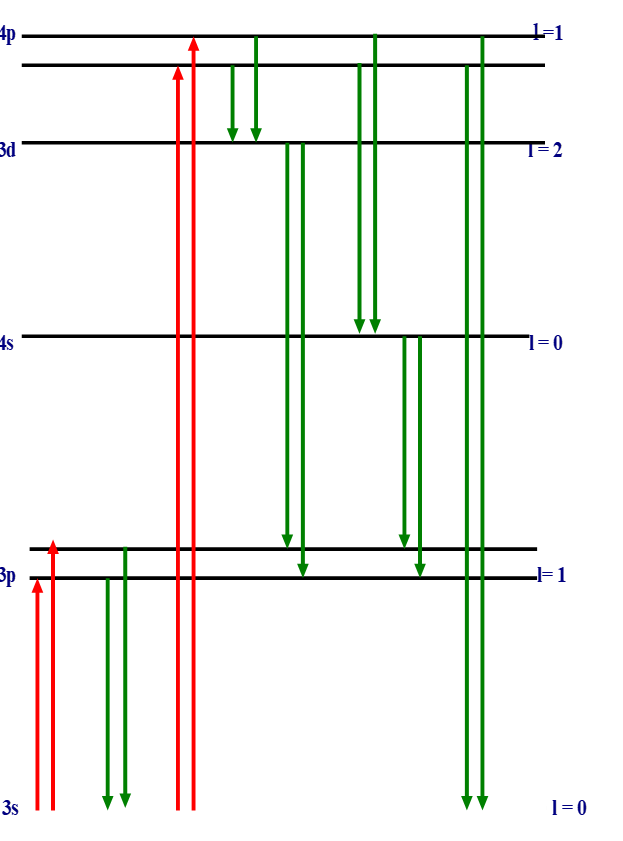
Du niveau 4p, l’électron a plusieurs possibilités pour revenir à l’état fondamental: directement ou par bonds successifs.

l’électron revient à 3s en perdant de l’énergie sous forme thermique ou en émettant une à plusieurs radiations électromagnétiques.

Les spectres

En regardant le diagramme, on voit que l’on aura des raies d’absorption et d’émission.

Le nombre de raies est plus important à l’émission qu’à l’absorption (où il est limité par les règles de sélection) spectre d’émission plus riche.

multiplicité des raies

On a des raies dédoublées (2 raies d’absorption pour chaque transition).

589,59 nm	330,30 nm
589,60 nm	330,23 nm

On a le même phénomène pour les raies d’émission.
Dédoublement dû au spin (s = +1/2 ou –1/2)

Raies de résonance

Parmi les transitions électroniques, une transition correspond au passage de l’état fondamental au niveau d’énergie immédiatement supérieur, puis retour au niveau le plus bas. C’est la raie de résonance: transition la plus probable.

Na : Raie de résonance.

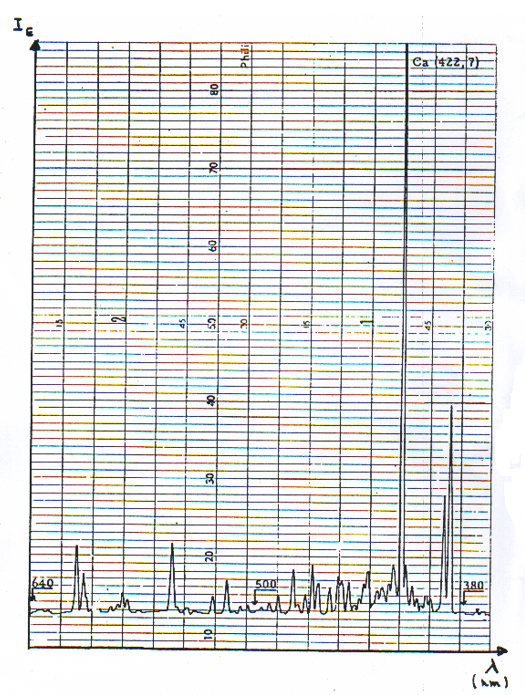
Cette raie est toujours caractéristique d’un élément ; c’est la plus intense. Dans l’exemple du Ca, elle se situe à 422,7 nm.
Il y a beaucoup de pics:

• 422,7nm : raie la plus intense ; elle correspond à la différence d’énergie la plus faible entre le niveau fondamental et le premier niveau d’énergie excité: résonance.
• Autres raies : niveaux supérieur.

Élargissement des raies

Causes d’élargissement

On n’a pas affaire à des raies mais à des pics.

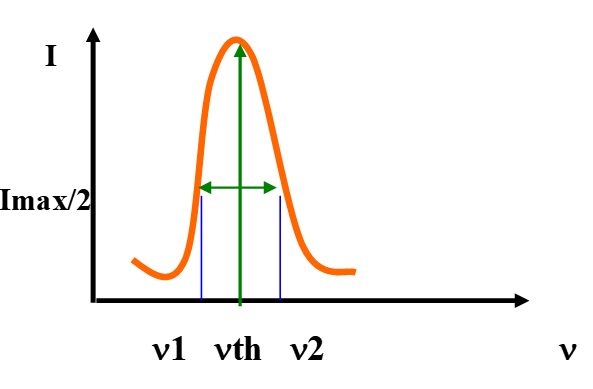
l’élargissement est mesurée à mi-hauteur du pic.

est dû à la vitesse de l’atome et au champ électrique où il se trouve.

Effet Doppler-Fizeau (effet de la vitesse)

En fonction de leur vitesse, les atomes donneront des raies de longueurs d’onde différentes. 
La variation de entre la raie observée pour un atome et [/latex]\lambda[/latex] moyenne est donnée par:

(1)  

Δλ=λm⋅VC⋅cosθ

C’est le principe du radar de la police: connaissant on mesure et on déduit V.

Effet Lorentz (effet de la pression)

Lorsque la pression augmente, les collisions entre les atomes sont plus nombreuses; cela implique une augmentation de la dispersion des vitesses des atomes élargissement.

Effet Stark (effet du champ électrique)

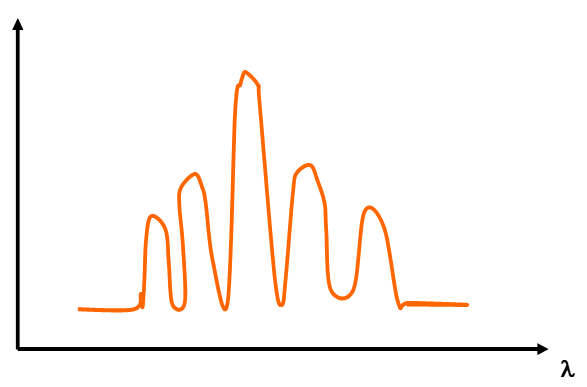
Lorsque l’on place un atome dans un champ électrique, la raie considérée se décompose en plusieurs raies réparties symétriquement autour de la raie théorique.

Positions des raies

On considère seulement la raie de résonance (mais cela est vrai pour toutes les raies).

On constate que la différence d’énergie ( ) entre le niveau d’énergie le plus bas et celui juste supérieur, augmente de gauche à droite dans la classification périodique (des alcalins aux gaz rares).

La longueur d’onde (nm) de la raie de résonance diminue:

1A	2A	3B	4B	5B	7B
Na	Mg	Al	Si	P	Cl
589	285	214	<200	<200	<200

N.B:

• on ne peut pas mesurer dans l’UV en dessous de 200 nm car les gaz atmosphériques absorbent (on ne peut pas doser des éléments comme Si, P, Cl).
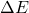• diminue de haut en bas dans un groupe

K	766 nm
Rb	780 nm
Cs	894 nm

Intensité des raies

Aspect qualitatif

Il peut être envisagé à partir de la loi de Boltzmann:

(2)  

Le nombre d’atomes à l’état excité Ni décroît de façon exponentielle quand la différence d’énergie entre l’état fondamental et l’état excité augmente.

augmente de gauche à droite et de bas en haut dans la classification périodique.

2000°C
Na
Zn

Conséquences: 

On dose en émission atomique, facilement les éléments situés à gauche et en bas dans la classification périodique, puisque pour avoir une raie d’émission, il faut de nombreux électrons à l’état excitée.

Le nombre d’atomes à l’état excité augmente quand la température augmente.

3000°C
Na
Zn

La sensibilité des méthodes à l’émission augmente lorsque la température augmente.

La stabilité de la température est une condition indispensable lorsque l’on fait une mesure d’autant que est grande.

La variation de 1000°C entraîne une sensibilité 60 fois plus grande pour Na et 70 000 fois pour Zn.  

Aspect quantitatif

En absorption atomique, on applique.
la loi de Beer – Lambert:

(3)  

Conditions:

• Phase vapeur
• Flamme ou four

En émission, l’intensité de la lumière émise est directement proportionnelle à la concentration de l’élément à doser.