Définition

La spectroscopie infrarouge est :

• une spectroscopie de bandes
• une méthode d’identification et de dosages non destructifs basée sur l’absorption des radiations électromagnétiques,
• 0,8 à 2,5 µm : 12500 – 4000 cm-1 : Proche IR
• 2,5 à 25 µm : 4000 – 400 cm-1 : Moyen IR
• 25 à 50 µm : 400 – 200 cm-1 : IR Lointain

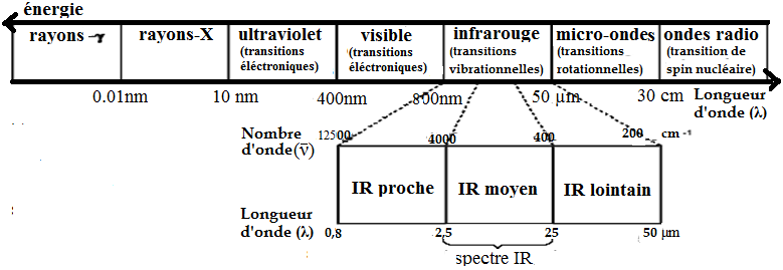
Étudie l’énergie de vibration associée ou pas à l’énergie de rotation des molécules

Moment dipolaire.

Fréquence de l’onde monochromatique identique à celle de la vibration.

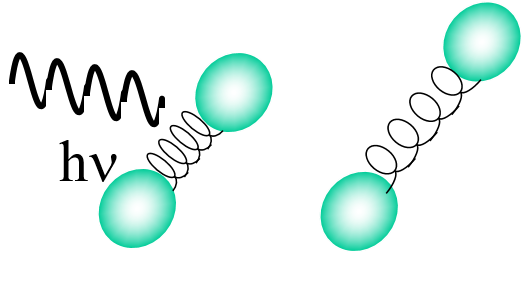
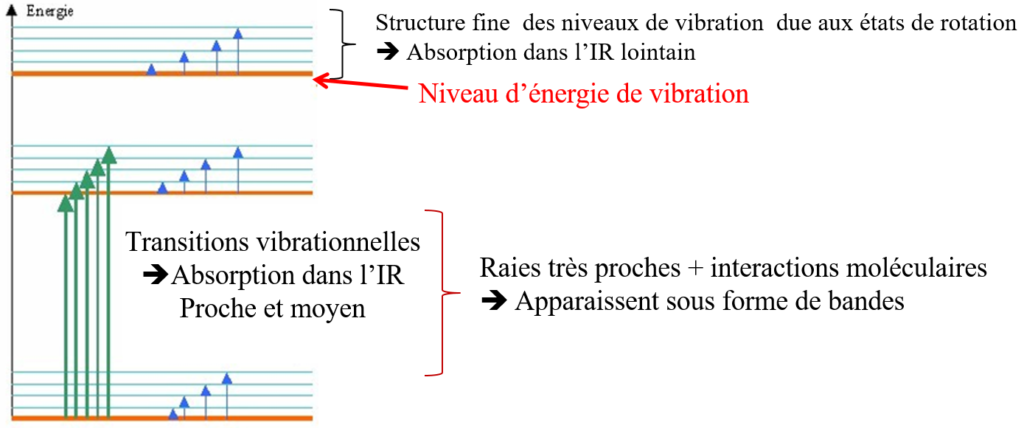
Théorie de l’absorption en infrarouge

Étude de la vibration

Modèle mécanique

Une masse liée à un ressort

Deux masses liées à un ressort

Nombre d’oscillations par unité de temps = la fréquence

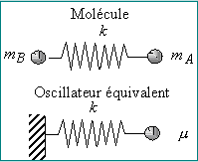
loi de Hooke

Avec

La grandeur pratique en spectroscopie vibrationnelle est le nombre d’onde.

Avec:

(1)  

Cas de la molécule HCl

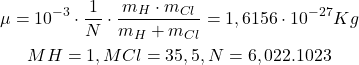
Loi de Hooke: exemples

La lumière de nombre d’onde 2900 cm^-1 excite l’état vibrationnel de la liaison de l’état fondamental au premier état excité. Calculer la constante de Hooke correspondant à la liaison

(2)  

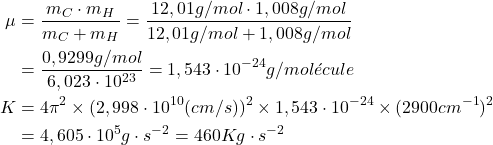
En mécanique classique
On considère qu’il n’y a pas de forces de frottement. Si on lâche le ressort, il oscille de manière infinie.

(3)  

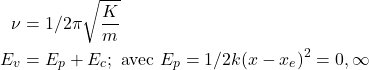
La courbe d’énergie potentielle en fonction de est une parabole.

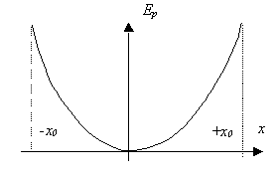
En mécanique quantique

(4)  

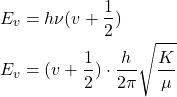
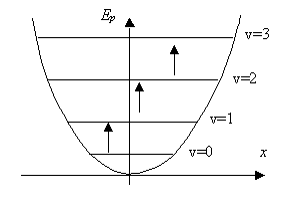
	nombre quantique de vibration
	0, 1, 2, 3, …
	± 1

Modèle moléculaire

Liaisons ne sont pas des ressorts parfaits
Niveaux de vibration de + en + rapprochés.

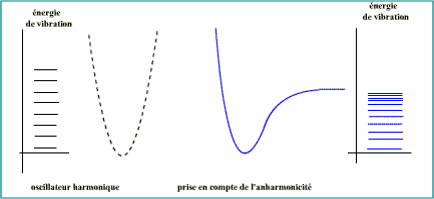
Étude de la rotation

Modèle mécanique

l’énergie de rotation :

(5)  

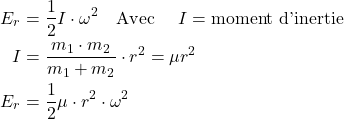
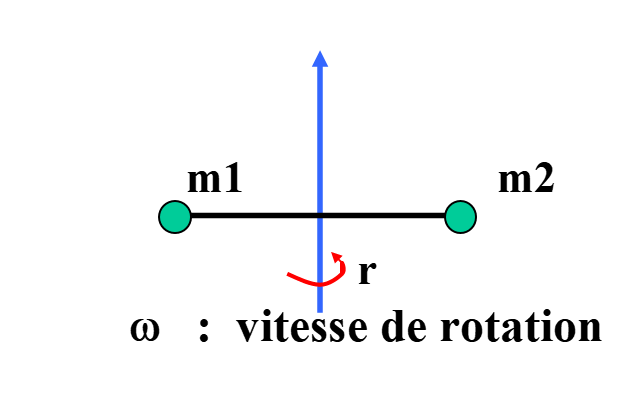
Modèle moléculaire

Dans ce cas ne peut prendre que certaines valeurs telle que :

(6)  

Énergie de rotation vibration:

Une molécule diatomique
à l’état (vibration+ rotation)

(7)  

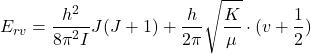
Les transitions

Caractéristiques générales

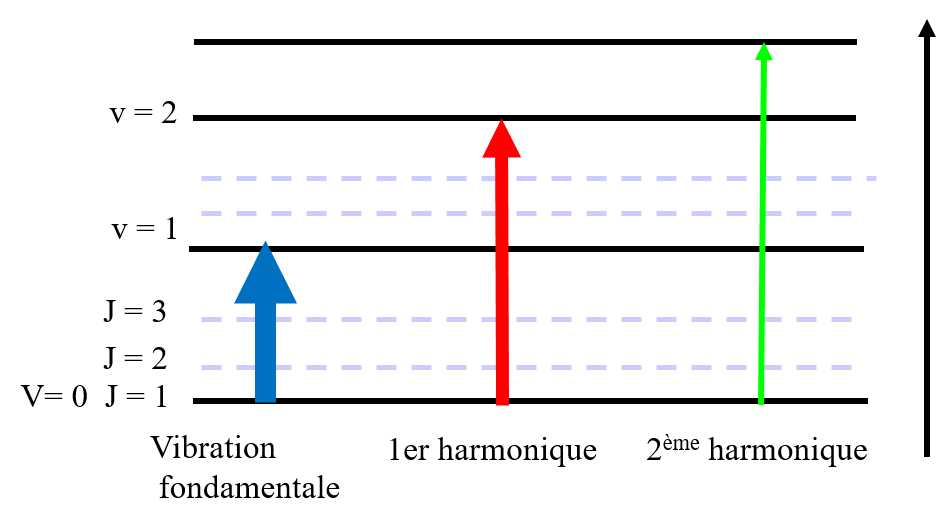
Vibration et bandes de spectre

Spectre IR = spectre de bandes
On obtient les bandes de vibration ou vibration – rotation fondamentales, harmoniques et de combinaison (v₁ + v₂)

• Abscisse : cm^-1
• Ordonnée : Transmittance (%T) ou Absorbance A = log(1/T)

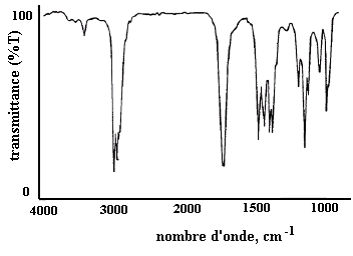
Conditions d’absorption

Pour qu’une bande soit active, il faut qu’il y ait un moment dipolaire entre les deux atomes

Les molécules homonucléaires (H₂, O₂, N₂) : inactives en IR
Toutes les vibrations ne se traduisent pas par une bande sur le spectre

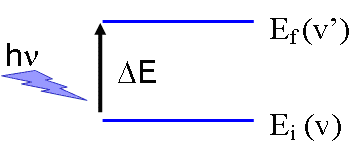
L’absorption a lieu à la résonance: c-à-d lorsque la fréquence de vibration de la liaison est égale à celle du rayonnement électromagnétique (REM).

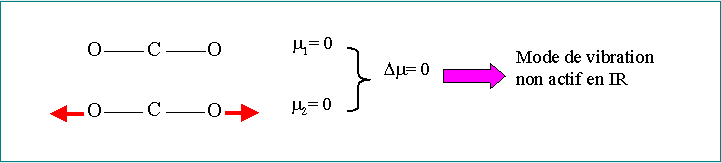
Nombre de bandes

N atomes	Degrés de liberté	Translation	Rotation	Vibration
Molécule linéaire	3N	3	2	3N-5
Molécule non-linéaire	3N	3	3	3N-6

Le degré de liberté est le nombre de coordonnées indépendantes nécessaire pour décrire le mouvement d’un objet

Molécule de N atomes reçoit de l’énergie :
il en résulte un mouvement de vibration compliqué, décomposé en mouvements plus simples appelés « Modes Normaux de Vibration »

Exemple :

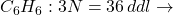• 30 modes de vibration
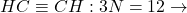• 7 modes de vibration

Modes de vibration

2 types :

• allongement
• déformation

Vibration d’allongement = « streching » 

modification de la longueur de liaison, sans modification de l’angle de la liaison.

il y a 2 modes : symétrique et antisymétrique

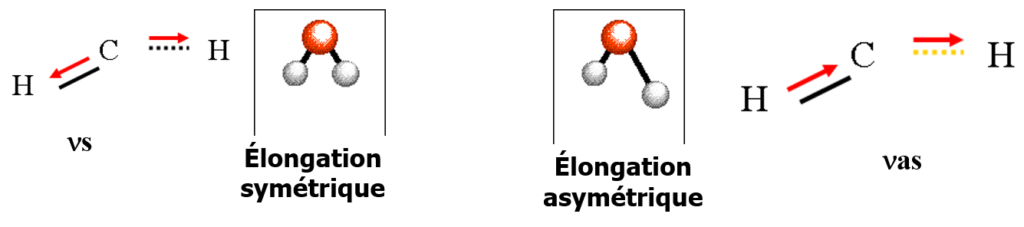
Déformation de l’angle « bending »
dans le plan ( )
hors du plan ( )
Ex: le benzène présente des déformations dans le plan et hors du plan.

Pour les structures linéaires triatomiques il existe:

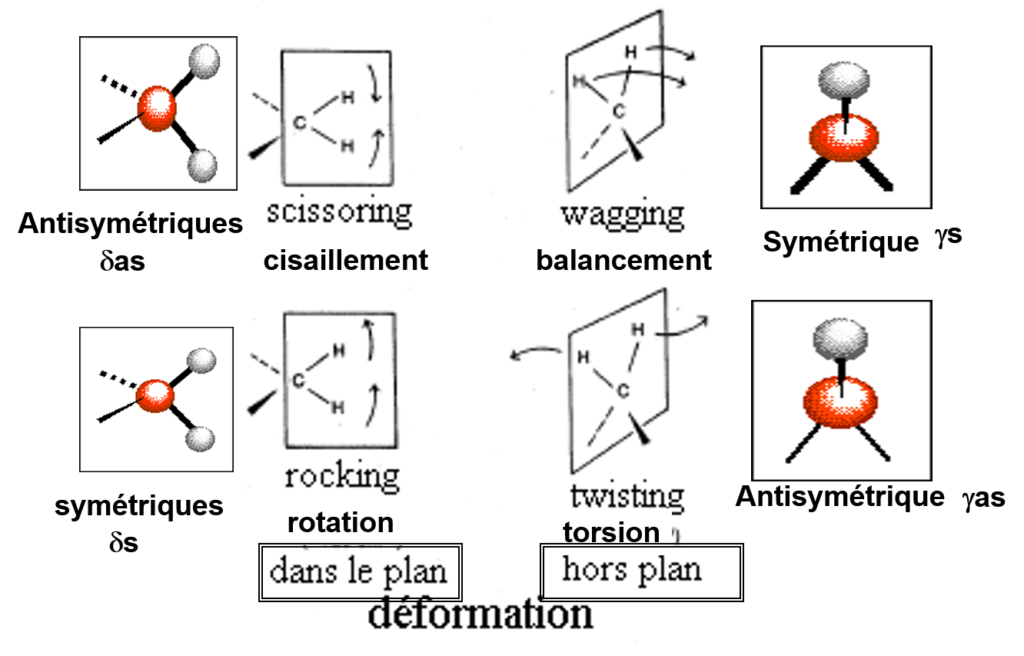
Pour les molécules polyatomiques, si elles sont symétriques, seules certaines vibrations seront actives.
Ex 1

il y a 9 – 5 = 4 modes de vibrations possibles:

• 1 vibration d’allongement symétrique:

Les oxygènes vibrent de façon symétrique (C immobile) : pas de dipôle crée; vibration inactive; pas de bande sur le spectre

• 1 vibration d’allongement antisymétriques

La vibration crée un dipôle par déformation de la molécule
on a une bande d’allongement sur le spectre. 

2 bandes de déformation: Une dans le plan
Une hors du plan
Une dégénérée donc une seule bande de déformation sur le spectre

Ex : 3×3 -5=4 modes de vibration

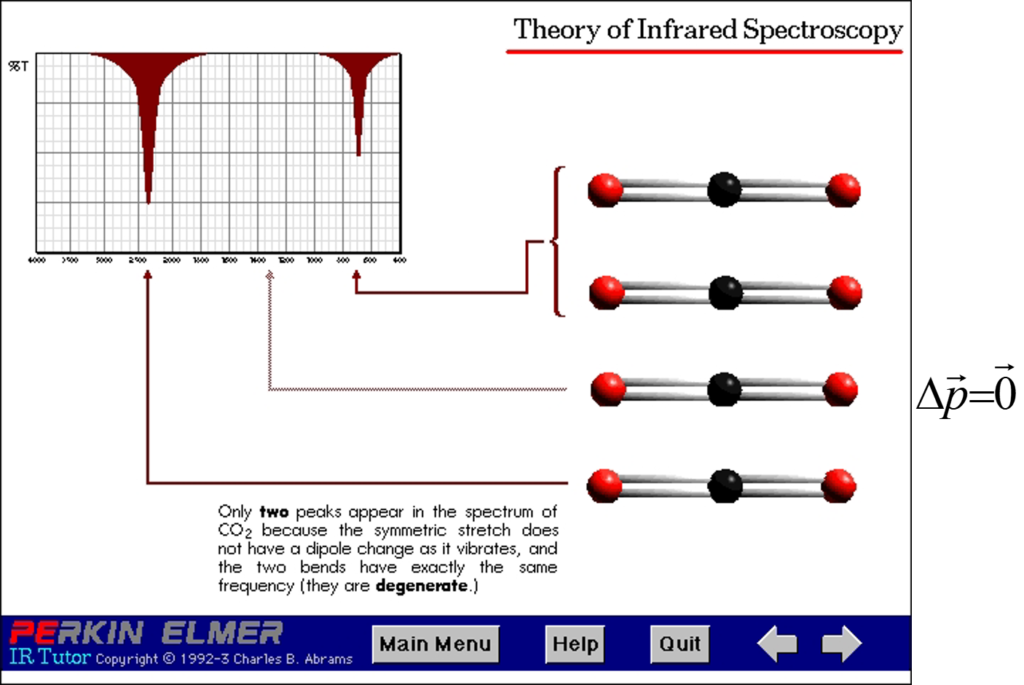
Ex2 : 9 – 6 = 3 modes de vibration

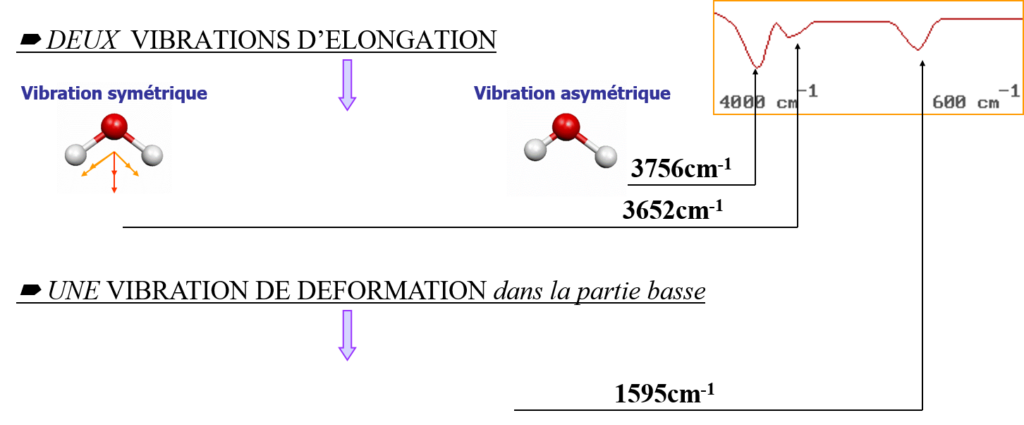
Position des bandes dans le spectre

Définition

Cela dépend de l’énergie absorbée ( )
Par ordre d’énergie décroissante, ou de nombre d’ondes décroissant on a:

• vibration d’allongement antisymétrique
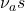
• vibration d’allongement symétrique
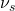
• vibration de déformation dans le plan
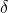
• vibration de déformation hors du plan

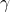
Facteurs influençant la position

Facteurs internes

(8)  

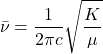
Il dépend de :

• la masse réduite 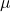du système A-B
• la constante de force de la liaison
• influence de k (augmente avec les liaisons multiples)
  Plus k est importante, plus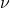 sera grande,
  Ex: 

Monoxyde de carbone	C O	2150 cm-1
Cétone	C = O	1715 cm-1
Alcools	C – O	1100 cm-1

	k (dyne/cm)		(cm-1)
C-C	4,6.10-5	1	1260 – 1100
C=C	10.10-5		1700 – 1600
CC	15.10-5		2250 – 2100

\begin{align} dyne/cm = g. cm. s^{-2} \qquad \qquad 1dyne = 10^{-5} N \end{align}

• influence de µ

Plus µ augmente, plus la fréquence diminue, plus le nombre d’ondes diminue.

(9)  

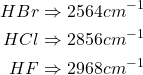
Vérification de bandes par deuterration :

\begin{align} \dfrac{\bar{\nu}_1}{\bar{\nu}_2}= \sqrt{\dfrac{\mu_1}{\mu_2}} \end{align}

(10)  

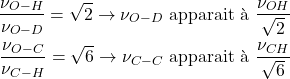
Couplage vibrationnel

un couplage entre des vibrations , qui conduit à une seule bande dans laquelle les deux groupements participent.
Exemple:

H – C = C –1620cm^-1 : Après deutération : D – C = C – : 1520 cm^-1

60 % de C = C

40 % à la C-H

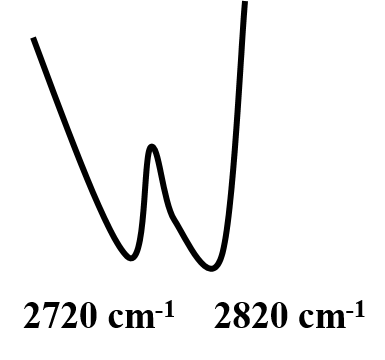
Bande de Fermi 

Il s’agit de l’interaction entre une vibration fondamentale et une vibration harmonique :

C-H aldéhyde : 2800 cm^-1 vibration fondamentale

2C-H aldéhyde : 2 x 1400  : vibration harmonique:

Donne le doublet caractéristique des aldéhydes

*Autres
Il y a des effets d’associations : par exemple, la formation de liaisons hydrogènes intermoléculaires.
Exemple d’acide carboxylique

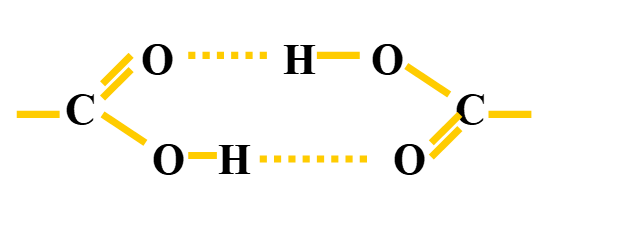
Cela provoque un élargissement des bandes et un déplacement vers les basses fréquences. De =3600cm^-1  à = 3400 cm^-1 

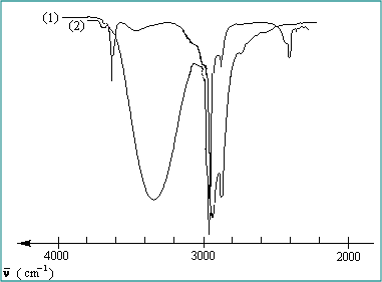
Produit pur

• Bande large entre 3200 cm-1 et 3400 cm-1 
• OH associé par liaison hydrogène : νOH associé

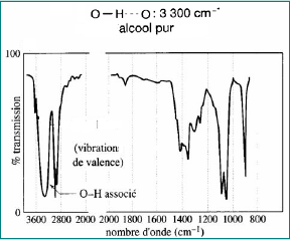
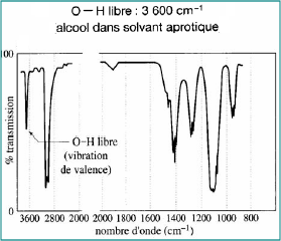
Dilution dans un solvant aprotique comme CCl4

• Bande large disparaît
• Apparition d’une bande fine, zone 3590-3650 cm-1 : νOH libre

-Facteurs externes

État physique

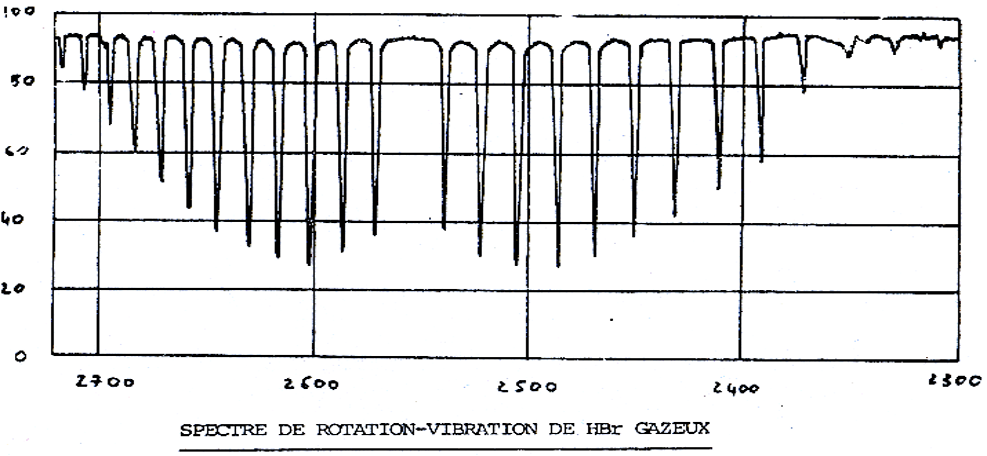
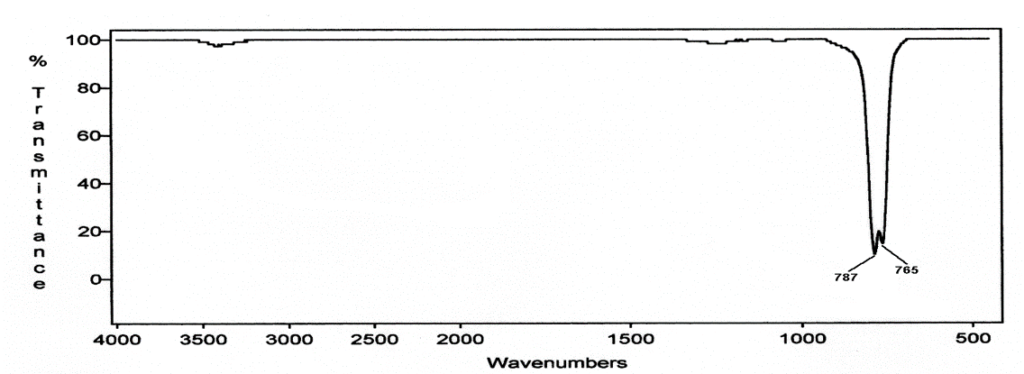
Sur un gaz, on obtient des bandes très fines car on voit les bandes de rotation. (voir spectre) : une bande de vibration est une multitude de raies de rotation.
En milieu liquide, on perd cette structure fine, par perte des bandes de rotation.

Solvant 

Selon le solvant, on a de faibles modifications (quelques cm^-1) sur la position des raies. Mais c’est important dans l’identification des composés.

Intensité des bandes

Intensité absolue

variable selon le type de vibration:

• Les bandes les plus intenses sont celles correspondant aux vibrations d’allongement
• Les bandes seront d’autant plus intenses que le moment dipolaire est grand.
• L’intensité d’une bande augmente avec la répétition d’un motif dans la molécule

Ex : cas de CH₂ et (CH₂)₅ : la bande (CH₂)₅ sera 5 fois plus intense que celle de CH₂ : I(CH₂)₅ =5 ICH₂

Intensité relative

Pour une même molécule, elle dépend de la concentration.
La loi de Beer-Lambert s’applique pleinement mais il est difficile de respecter la condition de dilution (en infrarouge, on est obligé de travailler avec des solutions concentrées).

MESURES

Instrumentation

Deux types:

• spectromètre dispersif: abandonné
• spectromètre à transformée de Fourier

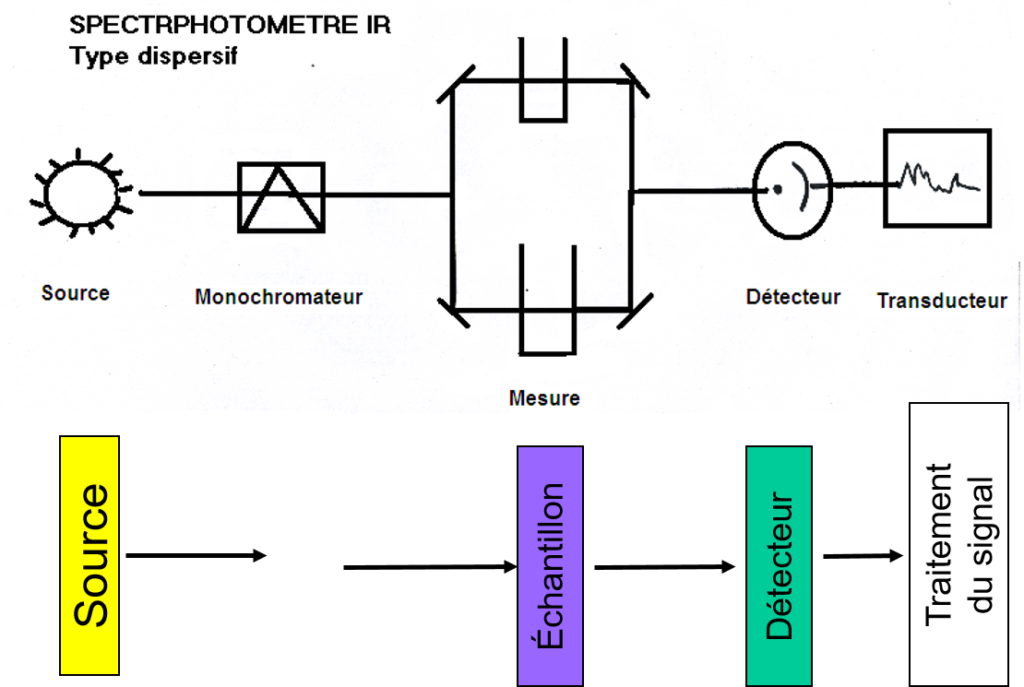
Source IR  

Il s’agit de filaments portés à incandescence (1500-2000°C) par effet Joule qui émettent des rayonnements IR.
On utilise des corps réfractaires : carbures, oxydes.

• oxydes de zirconium et yttrium = filament de Nernst (2000 K).
• carbure de silicium = lampe de Globar (1500 – 2000)

Résumé des caractéristiques des différentes sources IR

Source Domaine spectral (cm^-1) Domaine IR
Lampe W 10000 – 3000 Proche
Nernst 5000 – 300 Moyen
Globar 5000 – 30 Moyen + lointain
Lampe à vapeur de Hg 300 – 100 Lointain

Interféromètre:

Composé de:
un miroir fixe: MF
Un miroir mobile: MM
La séparatrice: miroir semi transparent
Principe: le REM IR arrive d’abord sur la séparatrice qui le divise en deux partie: 50% réfléchie sur le MF et 50% sur le MM
Les deux parties du REM vont interférer différemment selon la position du MM

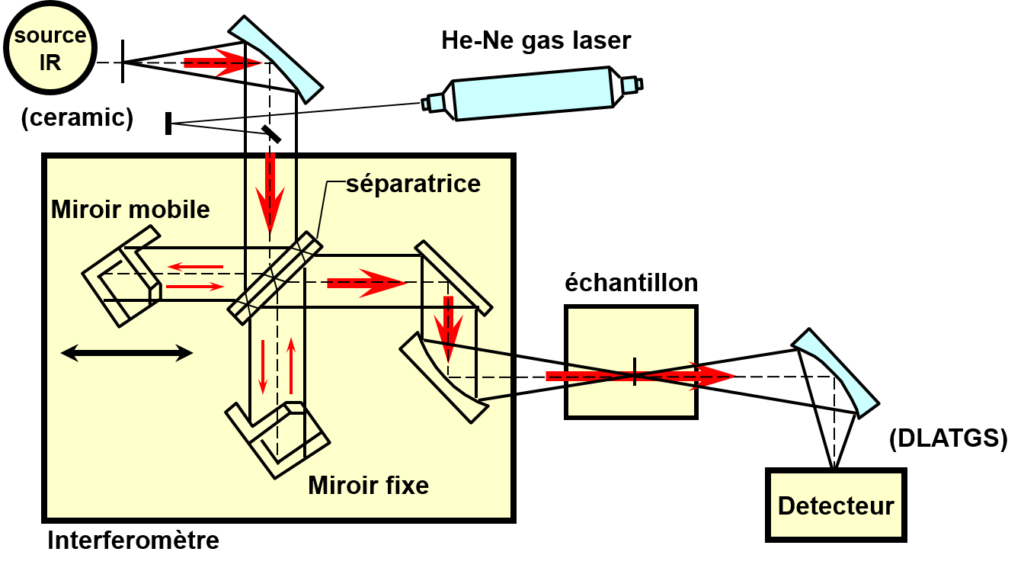
On obtient une intensité en fonction du déplacement du Miroir Mobile donc en fonction du temps: I = f(t)
I = f(t): interférogramme: signal sinusoidal

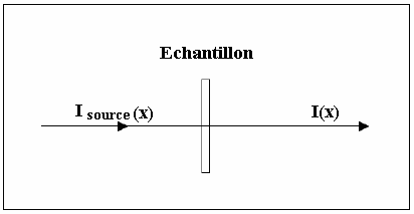
Echantillon:

l’échantillon subit ou non une transformation avant la mesure.
Cellules de mesure et optiques 
(pas de verre, quartz ou plastique). Les matériaux utilisés sont :

• NaCl, KBr (fragiles et solubles dans l’eau)
• CsI: transparent jusqu’à 200 cm-1
• AgCl, diamant, KRS-5 (bromoidure de thallium)
• Détecteur Cristal pyroélectrique, Photodiode
  Réponse rapide et suivi des modulations de l’intensité par l’interféromètre
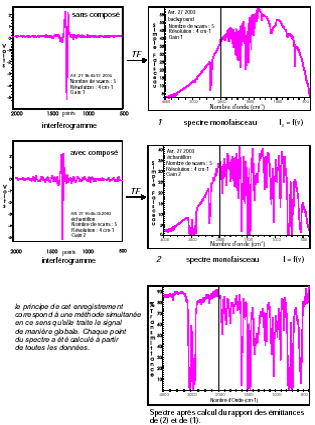
  *Traitement du signal
  Par informatique et logiciel adapté
  Le signal I = f(t) est traité par la fonction mathématique appelée TF
  On obtient I = f(\nu) = spectre IR

On réalise le spectre IR sans échantillon (S_b) , puis le spectre avec échantillon (S_e).

Le spectre sans bruit de fond est : S = S_e/S_b

Les spectres peuvent être stockés et traités (addition, soustraction…) et comparés à d’autres spectres (bibliothèque de spectres de référence).

Analyse des échantillons

Par transmission

On peut analyser des composés à l’état gazeux, solide, liquide.

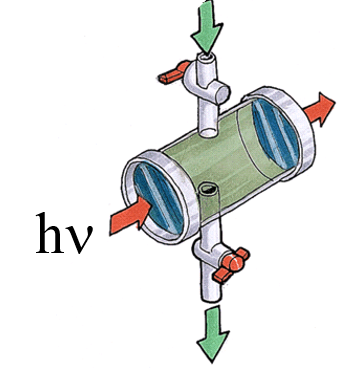
Etat gazeux

Dosage du CO et CO₂ du gaz d’échappement : respectivement à 2170 et 2350 cm_-1

On peut obtenir le spectre d’un gaz en permettant à l’échantillon de se répandre dans une cellule sous vide, appelée aussi cuve cylindrique. Ces cellules dont le trajet optique de quelques cm qui est parfois insuffisant pour les conditions de pression choisies; la cellule est alors de dimension plus importante et le faisceau optique est replié plusieurs fois à l’intérieur de la cellule par un jeu de miroirs interne.

État liquide 

2 solvants sont très utilisés :

• CCl4 : transparent entre 4000 et 1300 cm-1
• sulfure de carbone CS2 : transparent de 1300 à 400 cm-1

L’examen des liquides est généralement réalisé avec des cellules à parois démontables. Pour les observations on écrase modérément une goutte de l’échantillon entre deux disques de NaCl ou de KBr.
Les échantillons qui se présentent sous forme liquide à température ambiante sont habituellement analysés sous la forme pure ou en solution. Les solvants les plus courants sont le tétrachlorure de carbone (CCl4) et le sulfure de carbone (CS2).

Utilisation d’un film : plaque de KBr sur laquelle on fait un étalement du film liquide à analyser.

État solide

Certains composés ne peuvent pas être dissous :

• suspension dans l’huile de paraffine = NUJOL
• dispersion : pastillage
  on mélange le composé à analyser avec du KBr ( 1 à 2 % du composé, 98 à 99 % de KBr) obtention de poudre fine. On comprime ensuite cette poudre à l’aide d’une presse pour obtenir une petite pastille de 2 à 3 mm de diamètre, 1 mm d’épaisseur; on la place devant le faisceau IR.

Dispersion

On disperse quelques milligrammes d’échantillon dans une huile de paraffine (NUJOL) qui ne présente que des bandes d’absorption en dehors desquelles le spectre de l’échantillon est exploitable

Pastillage :

On broie le solide en présence de KBr dans un petit mortier, ensuite ce mélange est comprimé sous une pression de 5 à 8 tonnes/cm², avec une presse hydraulique ou manuelle. La pastille qui en résulte, d’aspect translucide est placée dans le porte échantillon.

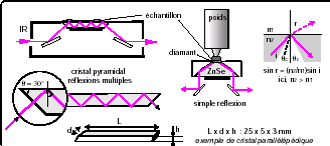
Par réflexion

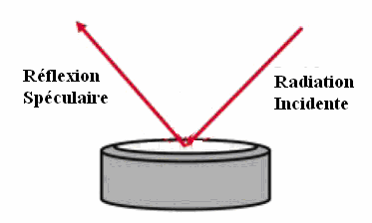
Réflexion spéculaire:

films de polymères, vernis, peintures

mesure de la lumière réfléchie dans une direction d’observation symétrique à celle d’incidence :

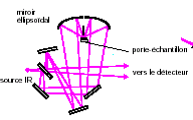
Réflexion diffuse

Poudres

Réflexion totale atténuée (ATR)

échantillon solide ou liquide sans préparation

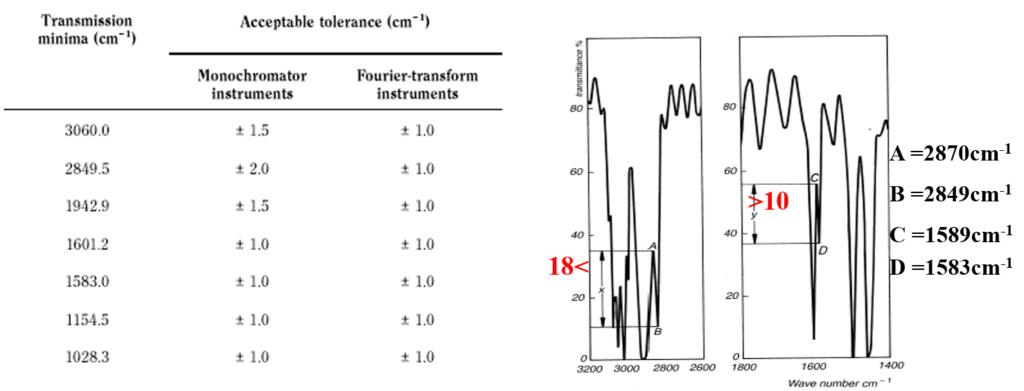
Contrôle

On contrôle en particulier l’exactitude de la longueur d’onde , et la résolution
Appareil IRTF: contrôle continu par laser:  
La Pharmacopée recommande un film en polystyrène : 14 maximums d’absorption, bandes très fines.

APPLICATIONS 

Analyse fonctionnelle

On cherche à déterminer les groupements chimiques d’une molécule afin de déterminer sa structure.  
Ceci est basé sur l’étude des spectres :

• position des bandes
• intensité des bandes
• largeur des bandes

On découpe le spectre en 6 zones et on va chercher à repérer les bandes principales (en général, ce sont des vibrations d’allongement).
Après, on cherche les bandes de déformation pour confirmer.

Zone A	à 3200 cm-1	Vibrations d’allongement,OH et NH ; bandes intenses et larges.
Zone B	entre 3000 et 3100 cm-1	=C-H (carbone avec une double liaison) bandes intenses et fines.
Zone C	de 2700 à 3000 cm-1	C-H (CH2, CH3 composés saturés), bandes intenses et fines
Zone D	de 1600 à 1800 cm-1	C = O; bandes intenses et fines
Zone E	de 1450 à 1600 cm-1	C = C; bandes faibles
Zone F	de 1000 à 1200 cm-1	C – O et \nu C-N ; bandes intenses et larges

Identification

Le spectre IR = empreinte digitale d’un composé. 
Médicaments, polymères, aliments
Analyse des lithiases: rénales, biliaires…

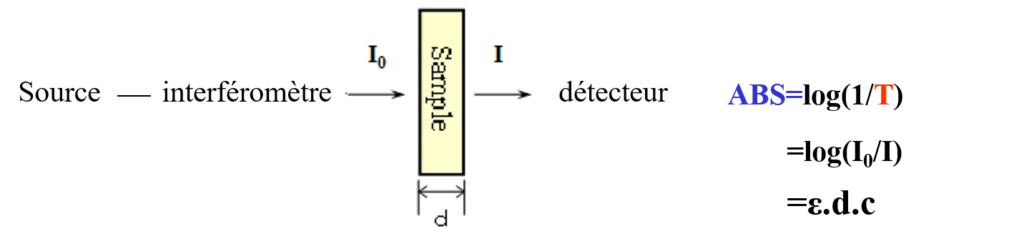
Analyse quantitative

Application de la loi de Beer Lambert en utilisant une bande caractéristique
peu précise

Quiz

[WpProQuiz 5]