\[ \begin{aligned} i_{Pb} = K_{Pb} \times C_{Pb} \\ i_{Cd} = K_{Cd} \times C_{Cd} \end{aligned} \]

\[ \Longrightarrow \dfrac{i_{Pb}}{i_{Cd}} = {\color{blue}K} \cdot \dfrac{C_{Pb}}{C_{Cd}} \]

\[ \begin{align*} \dfrac{1,58}{1,64} &= {\color{blue}K} \cdot \dfrac{4,18\times 10^{-5}}{3,23\times 10^{-5}}\\ {\color{blue}K} &= \dfrac{1,58}{1,64} \times \dfrac{3,23\times 10^{-5}}{4,18\times 10^{-5}} = 0,744 \end{align*} \]

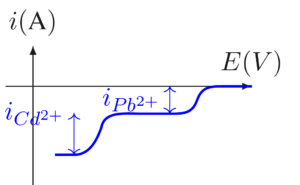
1. 2eme analyse: Détermination de la concentration de  ​\( Pb^{2+} \)​

\[ \begin{align} i_{Pb} = K_{Pb} \cdot {\color{red}C_{Pb}} \\ i_{Cd} = K_{Cd} \cdot C_{Cd} \Longrightarrow \dfrac{i_{Pb}}{i_{Cd}} = {\color{blue}K} \cdot \dfrac{\color{red}C_{Pb}}{C_{Cd}} \end{align} \]\( \begin{align*} {\color{red}C_{Pb}} &=\dfrac{i_{Pb}}{i_{Cd}} \times \dfrac{C_{Cd}}{\color{blue}K} = \dfrac{3}{2} \times \dfrac{ \dfrac{C_{Cd} \times 10 mL}{50 mL}}{\color{blue}0,744}\\ &=1,5 \times \dfrac{ \dfrac{3,23 \times 10^{-4} \times 10 mL}{50 mL}}{\color{blue}0,744}\\ &= 1,5 \times \dfrac{6,46 \times 10^{-5}}{\color{blue}0,744} = 1,5 \times 8,68 \times 10^{-5} = 130 \times 10^{-6} M \end{align*} \)